Question

【题目】已知抛物线的焦点为，准线为，是上一点，直线与抛物线交于，两点，若，则=

A.B.

C.D.

Answer 1

【答案】B

【解析】

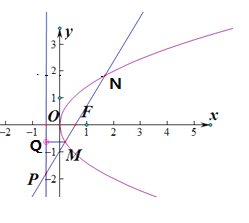
先根据题意写出直线的方程，再将直线的方程与抛物线y2＝2x的方程组成方程组，消去y得到关于x的二次方程，最后利用根与系数的关系结合抛物线的定义即可求线段AB的长．

解：抛物线C：y2＝2x的焦点为F（，0），准线为l：x＝﹣，设M（x1，y1），N（x2，y2），M，N到准线的距离分别为dM，dN，

由抛物线的定义可知|MF|＝dM＝x1+，|NF|＝dN＝x2+，于是|MN|＝|MF|+|NF|＝x1+x2+1．

∵，则，易知：直线MN的斜率为±，

∵F（，0），

∴直线PF的方程为y＝±（x﹣），

将y＝±（x﹣），代入方程y2＝2x，得3（x﹣）2＝2x，化简得12x2﹣20x+3＝0，

∴x1+x2，于是|MN|＝x1+x2+11

故选：B．