题目内容
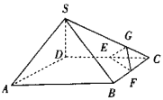
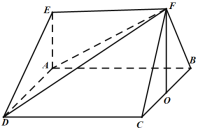
【题目】如图，在由三棱锥
和四棱锥
拼接成的多面体
中，
平面
，平面
平面，且是边长为
的正方形，
是正三角形.
（1）求证：
平面；
（2）若多面体的体积为
，求
与平面
所成角的正弦值.
【答案】（1）证明见解析.（2）
【解析】
（1）设点
为
中点，证明
平面
，又
平面，可以得到
，再由线面平行的判定定理，即可得到
平面
；
（2）由
求出
长，再以点
为原点建立直角坐标系，利用向量法求
与平面
所成角的正弦值.
（1）设点为中点，
是正三角形，所以
，
又平面
平面，且平面
平面
，
所以平面，
又平面，所以，
平面，
平面，所以平面；
（2）由题意，
，
解得
，
以点为原点建立如图直角坐标系，
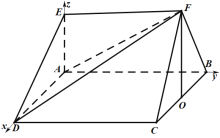
是边长为
的正方形，是正三角形.则
，
，
，
，
，
，
；
设平面的法向量为
，
则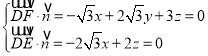
，
令
，则
，
，所以
，
设
与平面
所成角为
，
则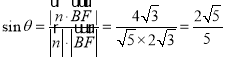
.
故直线与平面
所成角的正弦值为
.
练习册系列答案
相关题目
【题目】金秋九月，丹桂飘香，某高校迎来了一大批优秀的学生，新生接待其实也是和社会沟通的一个平台．校团委、学生会从在校学生中随机抽取了160名学生，对是否愿意投入到新生接待工作进行了问卷调查，统计数据如下：
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
（1）通过估算，试判断男、女哪种性别的学生愿意投入到新生接待工作的概率更大．
（2）能否有99%的把握认为，愿意参加新生接待工作与性别有关？
附：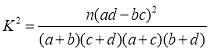
，其中
．
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
