Question

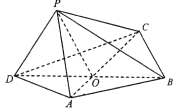
【题目】在正三棱柱中，,点D是BC的中点，点在上，且．

（1）求证： ∥平面；

（2）求证：平面⊥平面．

Answer 1

【答案】（1）详见解析 （2）详见解析

【解析】

试题分析：（1）证明线面平行，一般利用线面平行的判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证往往需要利用平面几何知识，如本题利用三角形中位线性质得到线线平行.设， 则是的中点，而已知是的中点，因此. （2）证明面面垂直，一般利用面面垂直的判定定理，即从线面垂直出发给予证明，而线面垂直的证明，往往需要多次利用线面垂直的性质定理与判定定理.由直三棱柱性质得侧棱垂直于底面，因此，由正三角形性质得，因此平面.从而. 又由平几何知识可得，因此平面.进而有平面⊥平面．

试题解析：（1） 记，连接.

∵四边形为矩形，∴是的中点，

又∵是的中点，∴.·······3分

又∵平面，平面，

∴∥平面.·······6分

（2）∵是正三角形，是的中点，

∴.

∵平面⊥平面，

平面平面，平面，

∴平面.·······9分

【或利用⊥平面，证明平面.】

∵平面，∴.

∵，，是中点，

∴，

∴，·······10分

∴，∴，

∴，又，平面，

∴平面.·······12分

又∵平面，∴平面平面．·······14分