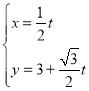题目内容
【题目】已知函数f（x）=|x2﹣2x﹣3|，若a＜b＜1，且f（a）=f（b），则u=2a+b的最小值为 ．
【答案】3﹣2 
【解析】解：作出f（x）的图象如图，由图可知，f（x）的对称轴为：x=1．
∵a＜b＜1且f（a）=f（b），
∴a＜﹣1，﹣1＜b＜1，
则|a2﹣2a﹣3|=|b2﹣2b﹣3|，
即a2﹣2a﹣3=﹣（b2﹣2b﹣3），
则（a﹣1）2+（b﹣1）2=8，a＜﹣1，﹣1＜b＜1，
则（a，b）的轨迹是圆上的一个部分，（黑色部分），
由u=2a+b得b=﹣2a+u，
平移b=﹣2a+u，当直线b=﹣2a+u和圆在第三象限相切时，截距最小，此时u最小，
此时圆心（1，1）到直线2a+b﹣u=0的距离d= 
，
即|u﹣3|=2 ，
得u=3﹣2 或u=3+2 （舍），
所以答案是：3﹣2 
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
【题目】在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：
物体重量（单位g） | 1 | 2 | 3 | 4 | 5 |
弹簧长度（单位cm） | 1.5 | 3 | 4 | 5 | 6.5 |
（1）画出散点图；
（2）利用公式（公式见卷首）求y对x的回归直线方程；
（3）预测所挂物体重量为8g时的弹簧长度．
