题目内容
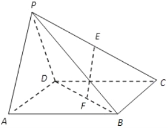
【题目】如图,已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,焦距为
,焦距为![]() ,点
,点![]() 是椭圆C上异于
是椭圆C上异于![]() 两点的动点,
两点的动点, ![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆C的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并作出证明.
的位置关系,并作出证明.
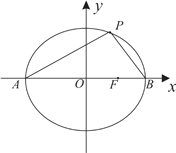
【答案】(1)![]() (2)以
(2)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
【解析】试题分析:(1)因为![]() 的面积最大值为
的面积最大值为![]() ,所以可列方程组
,所以可列方程组![]() 解得
解得![]() (2)直线与圆位置关系的判断,一般利用圆心到直线距离与半径大小进行判断, 设
(2)直线与圆位置关系的判断,一般利用圆心到直线距离与半径大小进行判断, 设![]() ,则可得直线PF方程,可得D点坐标,进而可得圆心,即BD中点坐标,再根据点到直线距离公式可得圆心到PF距离,最后与半径(BD一半)比较大小即可
,则可得直线PF方程,可得D点坐标,进而可得圆心,即BD中点坐标,再根据点到直线距离公式可得圆心到PF距离,最后与半径(BD一半)比较大小即可
试题解析:(1)由题意得, 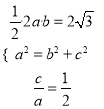 ,解得:
,解得: 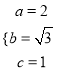 ,所以,椭圆方程为:
,所以,椭圆方程为: ![]() .
.
(2)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
证明:设直线![]() :
: ![]() ,则:
,则: ![]() ,
, ![]() 的中点为
的中点为![]() 为
为![]()
联立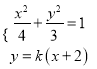 ,消去
,消去![]() 整理得:
整理得: ![]()
设![]() ,由韦达定理得:
,由韦达定理得: ![]() ,
,
解得: ![]() ,故有:
,故有: ![]()
又![]() ,所以当
,所以当![]() 时,
时, ![]() ,
, ![]() ,此时
,此时![]() 轴,
轴,
以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,
时, ![]() ,
,
所以直线![]()
![]() ,即:
,即: ![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离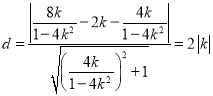
而![]() ,即知:
,即知: ![]() ,所以以
,所以以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.

练习册系列答案
相关题目
【题目】黄种人群中各种血型的人所占的比例如下:
血型 | A | B | AB | O |
该血型的人所占比例(%) | 28 | 29 | 8 | 35 |
已知同种血型的人可以输血,O型血可以输给任何一种血型的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?