题目内容
【题目】已知函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)设函数![]() 的图象与
的图象与![]() 轴交点为
轴交点为![]() ,曲线
,曲线![]() 在
在![]() 点处的切线方程是
点处的切线方程是![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)若函数![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
【答案】解:(Ⅰ)∵![]() ,
,
∴![]() . ……………………1分
. ……………………1分
∵![]() 在
在![]() 处切线方程为
处切线方程为![]() ,
,
∴![]() , ……………………3分
, ……………………3分
∴![]() ,
,![]() . (各1分) ……………………5分
. (各1分) ……………………5分
(Ⅱ)![]()
![]()
![]() .
.
![]()
![]()
![]() . ……………………7分
. ……………………7分
①当![]() 时,
时,![]() ,
,

![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() . ……………………9分
. ……………………9分
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ……………………10分
……………………10分
(ⅰ)当![]() ,即
,即![]() 时,
时,

![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() ;……11分
;……11分
(ⅱ)当![]() ,即
,即![]() 时,
时,![]()
![]() ,
,
故![]() 在
在![]() 单调递减; ……12分
单调递减; ……12分
(ⅲ)当![]() ,即
,即![]() 时,
时,

![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递 ………13分
上单调递 ………13分
综上所述,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() .
.
(“综上所述”要求一定要写出来)
【解析】
试题(I)根据曲线y=f(x)在A点处的切线方程是y=3x-3,建立关于a和b的方程组,解之即可;
(II)先求出函数g(x)的解析式,然后讨论a的正负,利用导数的符号研究函数的单调性,根据fˊ(x)>0和fˊ(x)<0求出函数g(x)的单调区间即可.
试题解析:(Ⅰ)∵![]() ,
,
∴![]() .
.
∵![]() 在
在![]() 处切线方程为
处切线方程为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .(各1分)
.(各1分)
(Ⅱ)![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
①当![]() 时,
时,![]() ,
,
|
| 0 |
|
| - | 0 | + |
|
| 极小值 |
|
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]()
(ⅰ)当![]() ,即
,即![]() 时,
时,
|
| 0 |
|
|
|
| - | 0 | + | 0 | - |
|
| 极小值 |
| 极大值 |
|
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() ;
;
(ⅱ)当![]() ,即
,即![]() 时,
时,![]()
![]() ,
,
故![]() 在
在![]() 单调递减;
单调递减;
(ⅲ)当![]() ,即
,即![]() 时,
时,
|
|
|
| 0 |
|
| - | 0 | + | 0 | - |
|
| 极小值 |
| 极大值 |
|
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减
上单调递减
综上所述,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() .
.
(“综上所述”要求一定要写出来)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某高校共有10000人,其中男生7500人,女生2500人,为调查该校学生每则平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).调查部分结果如下![]() 列联表:
列联表:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | 35 | ||
每周平均体育运动时间超过4小时 | 30 | ||
总计 | 200 |
(1)完成上述每周平均体育运动时间与性别的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 把握认为“该校学生的每周平均体育运动时间与性别有关”;
把握认为“该校学生的每周平均体育运动时间与性别有关”;
(2)已知在被调查的男生中,有5名数学系的学生,其中有2名学生每周平均体育运动时间超过4小时,现从这5名学生中随机抽取2人,求恰有1人“每周平均体育运动时间超过4小时”的概率.
附: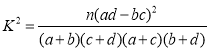 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |