题目内容
【题目】(1)在复数范围内解方程![]() (
(![]() 为虚数单位)
为虚数单位)
(2)设![]() 是虚数,
是虚数,![]() 是实数,且
是实数,且![]()
(i)求![]() 的值及
的值及![]() 的实部的取值范围;
的实部的取值范围;
(ii)设![]() ,求证:
,求证:![]() 为纯虚数;
为纯虚数;
(iii)在(ii)的条件下求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ;
;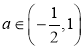 (ii)证明见解析;(iii)
(ii)证明见解析;(iii)![]()
【解析】
(1)利用待定系数法,结合复数相等构造方程组来进行求解;(2)(i)采用待定系数法,根据实数的定义构造方程即可解得![]() 和
和![]() ,利用
,利用![]() 的范围求得
的范围求得![]() 的范围;(ii)利用复数的运算进行整理,根据纯虚数的定义证得结论;(iii)将
的范围;(ii)利用复数的运算进行整理,根据纯虚数的定义证得结论;(iii)将![]() 整理为
整理为![]() ,
,![]() ,利用基本不等式求得最小值.
,利用基本不等式求得最小值.
(1)
设![]() ,则
,则![]()
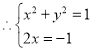 ,解得:
,解得: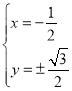
![]()
(2)(i)设![]()
![]() 且
且![]()
![]()
![]() 为实数
为实数 ![]() ,整理可得:
,整理可得:![]()
即![]()
![]()
![]()
(ii)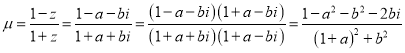
由(i)知:![]() ,则
,则![]()
![]() 且
且![]()
![]()
![]() 是纯虚数
是纯虚数
(iii)
令![]() ,则
,则![]() ,
,![]()
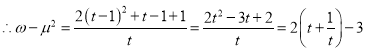
![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号) ![]()
即![]() 的最小值为:
的最小值为:![]()

练习册系列答案
相关题目
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知点
.已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)求![]() 的值;
的值;
(2)若直线![]() 是过定点
是过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 作
作![]() 的垂
的垂
线与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
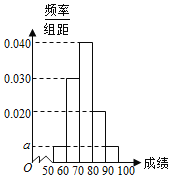
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图![]() 如图所示
如图所示![]() ,规定80分及以上者晋级成功,否则晋级失败.
,规定80分及以上者晋级成功,否则晋级失败.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
![]() Ⅰ
Ⅰ![]() 求图中a的值;
求图中a的值;
![]() Ⅱ
Ⅱ![]() 根据已知条件完成下面
根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“晋级成功”与性别有关?
的把握认为“晋级成功”与性别有关?
![]() Ⅲ
Ⅲ![]() 将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望
将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望![]() 与方差
与方差![]() .
.
![]() 参考公式:
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|