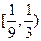题目内容
已知命题 函数
函数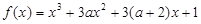 有极值;命题
有极值;命题 函数
函数 且
且 恒成立.若
恒成立.若 为真命题,
为真命题, 为真命题,则
为真命题,则 的取值范围是
的取值范围是
 函数
函数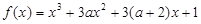 有极值;命题
有极值;命题 函数
函数 且
且 恒成立.若
恒成立.若 为真命题,
为真命题, 为真命题,则
为真命题,则 的取值范围是
的取值范围是A. | B. | C.  | D. |
C
 为真命题,
为真命题, 为真命题,可得
为真命题,可得 为假命题,
为假命题, 为真命题
为真命题 为假命题,即函数
为假命题,即函数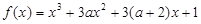 无极值,可得
无极值,可得它的导函数
 无解,即
无解,即 ,
,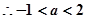
 为真命题,即对任意的
为真命题,即对任意的 都有不等式
都有不等式 恒成立,所以有
恒成立,所以有
 ,令
,令 ,
, ,解得x=-1
,解得x=-1 ,所以
,所以 在
在 单调递增,
单调递增, ,所以
,所以 在
在 单调递减,所以
单调递减,所以 的最大值就为
的最大值就为
 ,所以
,所以
所以


练习册系列答案
相关题目
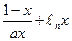 在[1,+∞
在[1,+∞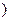 上为增函数.
上为增函数. 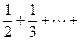
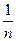
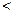
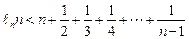 (n∈N*且n ≥ 2 )
(n∈N*且n ≥ 2 ) .
.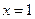 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出 关于
关于 的关系式(用
的关系式(用 ,函数
,函数 .若存在
.若存在 使得
使得 成立,求
成立,求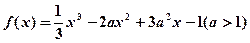 。
。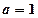 时,求函数
时,求函数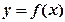 的单调增区间;
的单调增区间;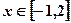 , 恒有
, 恒有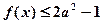 ,求
,求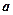 的取值范围。
的取值范围。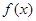 的图象如图所示,则不等式
的图象如图所示,则不等式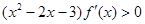 的解集为
的解集为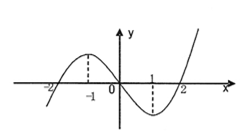




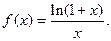
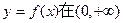 上的单调性;
上的单调性;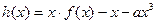 在(0,2)上有极值,求
在(0,2)上有极值,求 的取值范围。
的取值范围。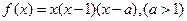
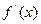 ; 并证明
; 并证明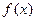 有两个不同的极值点
有两个不同的极值点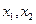 ;
; 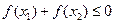 成立,求
成立,求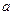 的取值范围.
的取值范围. ,若
,若 ,则
,则 ( )
( )



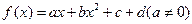 的导函数
的导函数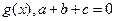 ,且
,且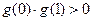 设
设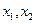 是方程
是方程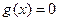 的两根,则|
的两根,则|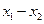 |的取值范围为
|的取值范围为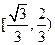 B
B 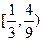 C
C 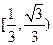 D
D