��Ŀ����
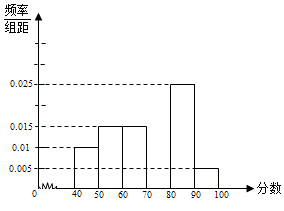
����Ŀ��ijУ�߶�������N��ѧ�������������ɼ�������120�֣��ֲ�ֱ��ͼ��ͼ����֪������100��110��ѧ������21�ˣ� ������������N�ͷ�����110��115�ֵ�����n��
���������ӷ�����110��115�ֵ�n��ѧ����Ů��ռ ![]() ������ѡ2�ˣ�������ǡ�ú���һ��Ů���ĸ��ʣ�
������ѡ2�ˣ�������ǡ�ú���һ��Ů���ĸ��ʣ�
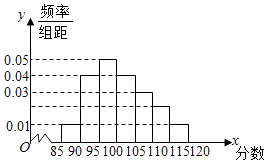
����Ϊ�˷���ij��ѧ����ѧϰ״̬��������һ�ε�ѧϰ�ṩָ���Խ��飬����ǰ7�ο��Ե���ѧ�ɼ�x������150�֣��������ɼ�y���з����������Ǹ���7�ο��Եijɼ���
��ѧ | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
���� | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
��֪�����������ɼ�y����ѧ�ɼ�x��������صģ�����������ѧ�ɼ��ﵽ130�֣�����������������ɼ���Լ�Ƕ��٣�
��������һ�����ݣ�u1 �� v1������u2 �� v2��������un �� vn������ع���v=��+��u��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ 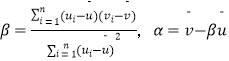 ��
��
���𰸡��⣺��������100��110�ڵ�ѧ����Ƶ��Ϊ
P1=��0.04+0.03����5=0.35����1�֣�
���Ըð�������Ϊ ![]() ��
��
������110��115�ڵ�ѧ����Ƶ��Ϊ
P2=1����0.01+0.04+0.05+0.04+0.03+0.01����5=0.1��
������110��115�ڵ�ѧ��������Ϊn=60��0.1=6��
���������������110��115����6��ѧ��������Ů����2����
������ΪA1��A2��A3��A4��Ů��ΪB1��B2��
��6��ѧ����ѡ��2�˵Ļ����¼�Ϊ
��A1��A2������A1��A3������A1��A4������A1��B1������A1��B2����
��A2��A3������A2��A4������A2��B1������A2��B2����
��A3��A4������A3��B1������A3��B2����
��A4��B1������A4��B2������B1��B2������15����
����ǡ�ú���һ��Ů���Ļ����¼�Ϊ
��A1��B1������A1��B2������A2��B1������A2��B2����
��A3��B1������A3��B2������A4��B1������A4��B2������8����
��������ĸ���Ϊ ![]() ��
��
������ ![]() ��
��
![]() ��
��
����x��y֮�����������ع�ϵ�����ݻع�ϵ����ʽ�õ�
![]() ��
��
�������Իع鷽��Ϊ ![]() ��
��
��x=130ʱ������ ![]() ��
��
���Թ������������ɼ���Լ��115�֣�
��������������Ƶ�ʡ�Ƶ�������������Ĺ�ϵ�������Ӧ����ֵ���������������оٷ���������¼�����������ĸ���ֵ��������ƽ�����ͻع�ϵ����д�����Իع鷽�̣����÷�����x=130ʱ ![]() ��ֵ��
��ֵ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�