题目内容
【题目】已知圆C：x2+y2=12，直线l：4x+3y=25．求圆C上任意一点A到直线l的距离小于2的概率．
【答案】解：设直线l'：4x+3y﹣C=0，
l'与直线l：4x+3y=25的距离等于2，且与已知圆相交，
得 
=2，解之得C=15或35
∵C＜25，可得C=15
∴到直线l：4x+3y=25的距离等于2且与已知圆相交的直线
为直线l'：4x+3y﹣15=0，
设l'交圆x2+y2=12于E、B两点，过圆心作EB的垂线，垂足为D，
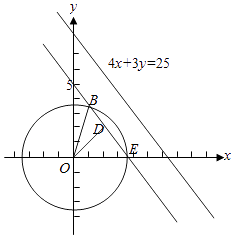
则D为EB的中点，
∵|OD|= 
=3，
∴Rt△EOD中，cos∠EOD= 
= 
，得∠EOD=30°
由此可得∠EOB=60°
当圆C上任意一点A到直线l的距离小于2时，点A位于劣弧BE上，
因此，所求概率为P= 
= 
．
【解析】根据平行线的距离公式，算出到直线l：4x+3y=25的距离等于2且与已知圆相交的直线为直线l'：4x+3y﹣15=0．设l'交圆x2+y2=12于E、B两点，由图形观察可得当动点A位于劣弧BE上时点A到直线l的距离小于2．由此利用点到直线的距离公式，结合垂径定理和三角函数的定义算出∠EOB=60°，即可得到所求概率．
【考点精析】关于本题考查的几何概型，需要了解几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能得出正确答案．
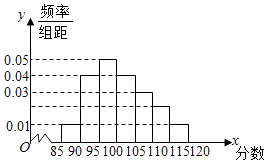
【题目】某校高二奥赛班N名学生的物理测评成绩（满分120分）分布直方图如图，已知分数在100～110的学生数有21人． （Ⅰ）求总人数N和分数在110～115分的人数n；
（Ⅱ）现准备从分数在110～115分的n名学生（女生占 
）中任选2人，求其中恰好含有一名女生的概率；
（Ⅲ）为了分析某个学生的学习状态，对其下一阶段的学习提供指导性建议，对他前7次考试的数学成绩x（满分150分），物理成绩y进行分析，下面是该生7次考试的成绩．
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的，若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？
附：对于一组数据（u1 ， v1），（u2 ， v2），，（un ， vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为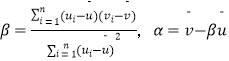 
．
