题目内容
【题目】在公差大于0的等差数列{an}中，2a7﹣a13=1，且a1 ， a3﹣1，a6+5成等比数列，则数列{（﹣1）n﹣1an}的前21项和为（ ）
A.21
B.﹣21
C.441
D.﹣441
【答案】A
【解析】解：公差d大于0的等差数列{an}中，2a7﹣a13=1，
可得2a1+12d﹣（a1+12d）=1，即a1=1，
a1，a3﹣1，a6+5成等比数列，
可得（a3﹣1）2=a1（a6+5），
即为（1+2d﹣1）2=1+5d+5，
解得d=2（负值舍去）
则an=1+2（n﹣1）=2n﹣1，n∈N*，
数列{（﹣1）n﹣1an}的前21项和为a1﹣a2+a3﹣a4+…+a19﹣a20+a21=1﹣3+5﹣7+…+37﹣39+41
=﹣2×10+41=21．
故选：A．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系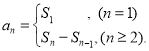
才能正确解答此题．
尖子生新课堂课时作业系列答案
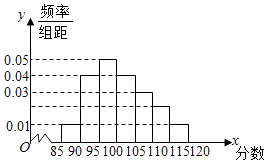
英才计划同步课时高效训练系列答案
【题目】某校高二奥赛班N名学生的物理测评成绩（满分120分）分布直方图如图，已知分数在100～110的学生数有21人． （Ⅰ）求总人数N和分数在110～115分的人数n；
（Ⅱ）现准备从分数在110～115分的n名学生（女生占 
）中任选2人，求其中恰好含有一名女生的概率；
（Ⅲ）为了分析某个学生的学习状态，对其下一阶段的学习提供指导性建议，对他前7次考试的数学成绩x（满分150分），物理成绩y进行分析，下面是该生7次考试的成绩．
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知该生的物理成绩y与数学成绩x是线性相关的，若该生的数学成绩达到130分，请你估计他的物理成绩大约是多少？
附：对于一组数据（u1 ， v1），（u2 ， v2），，（un ， vn），其回归线v=α+βu的斜率和截距的最小二乘估计分别为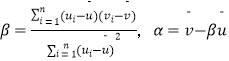 
．
