题目内容
(本小题满分12分)如图所示,已知六棱锥 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
(Ⅰ)求证:平面 //平面
//平面 ;
;
(Ⅱ)设 ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
的值。
(Ⅰ)只需证OM//PD, BE//DC;(Ⅱ) .
.
解析试题分析:(Ⅰ)连接AD交BE与点O,连接OM,因为 是
是 的中点,O为AD的中点,所以OM//PD,在正六边形
的中点,O为AD的中点,所以OM//PD,在正六边形 中,BE//DC,又BE∩OM=O,PD∩DC=D,所以平面
中,BE//DC,又BE∩OM=O,PD∩DC=D,所以平面 //平面
//平面 。
。
(Ⅱ)以A为原点,AE、AB、AP所在直线分别为 轴,建立空间直角坐标系,设AB=a,则AP=
轴,建立空间直角坐标系,设AB=a,则AP= ,所以
,所以 ,
, ,设面DME的法向量为
,设面DME的法向量为 ,面FME的法向量为
,面FME的法向量为 ,则
,则 ,
, ,
,
因为二面角 的大小为
的大小为 ,所以
,所以 ,解得
,解得 .
.
考点:线面垂直的性质定理;面面平行的判定定理;二面角。
点评:用向量法求二面角,优点是思维含量少,确定是计算较为复杂。因为我们再用向量法求二面角时,一定要认真、仔细。避免出现计算错误。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 中,
中, ,
, ,
, 是角平分线。求证:
是角平分线。求证: 。
。

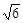 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记 ,用
,用 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.


 中,
中, ,
, ,
, .
.
 ;(2)
;(2) .
. 中,侧面
中,侧面
 底面ABC,侧面
底面ABC,侧面 ,E、F分别是
,E、F分别是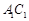 、AB的中点.
、AB的中点.
 ;
; 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,
 ,且
,且 点满足
点满足 .
. 
 平面
平面 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,确定点
?若存在,确定点