题目内容
(本题满分10分)
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=3,OC=4,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A-BE-C的余弦值.
(1)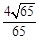 (2)
(2)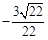
解析试题分析:解:(I)以O为原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系.
则有A(0,0,2),B(3,0,0),C(0,4,0),E(0,2,0).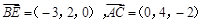
所以,cos<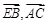 >
>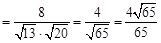 . ……………………3分
. ……………………3分
由于异面直线BE与AC所成的角是锐角,
所以,异面直线BE与AC所成角的余弦值是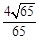 . ……………………5分
. ……………………5分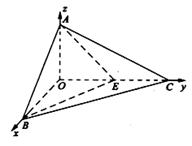
(II)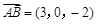 ,
,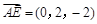 ,
,
设平面ABE的法向量为 ,
,
则由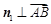 ,
,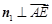 ,得
,得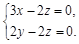 ,
,
取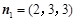 ,
,
又因为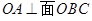
所以平面BEC的一个法向量为n2=(0,0,1),
所以 . ……………………8分
. ……………………8分
由于二面角A-BE-C的平面角是n1与n2的夹角的补角,
所以,二面角A-BE-C的余弦值是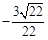 .……………………10分
.……………………10分
考点:本试题考查了异面直线的角和二面角的求解。
点评:对于角的求解问题,一般分为三步进行,一作,二证,三解答。因此要掌握角的表示,结合定义法和性质来分析得到角,进而求解,属于基础题。

练习册系列答案
相关题目

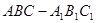 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,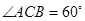 ,E、F分别是
,E、F分别是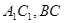 的中点。
的中点。
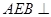 平面
平面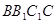 ;
;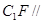 平面ABE;
平面ABE;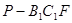 的体积。
的体积。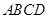 所在平面与平面
所在平面与平面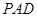 垂直,
垂直,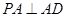 ,且
,且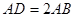 ,
,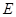 为
为 上的动点.
上的动点.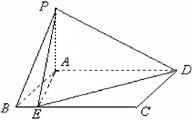
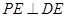 ;
; ,在线段
,在线段 的大小为
的大小为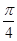 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由. 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
 //平面
//平面 ;
; ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
的值。 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
. 中,
中,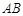 ∥
∥ ,
, ,
, ,
,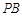 ⊥
⊥ ,
, ⊥
⊥ 为
为 的中点.
的中点.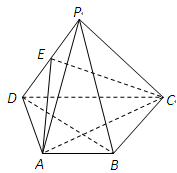
 ∥平面
∥平面 ;
; .
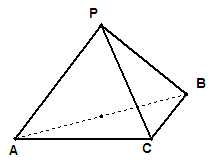
.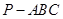 中,
中,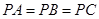 ,
,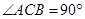 ,
,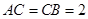 .
. 
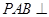 平面
平面 ;
;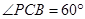 时,求三棱锥
时,求三棱锥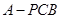 的体积.
的体积. 为圆
为圆 的直径,点
的直径,点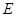 、
、 在圆
在圆 ,矩形
,矩形 所在的平面与圆
所在的平面与圆 ,
, .
.
 平面
平面 ;
;  的长为何值时,平面
的长为何值时,平面 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为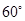 ?
?