题目内容
如图所示,在直三棱柱ABC-A1B1C1中, AC⊥BC.
(1) 求证:平面AB1C1⊥平面AC1;
(2) 若AB1⊥A1C,求线段AC与AA1长度之比;
(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.
(1) 直三棱柱中,所以B1C1⊥CC1; 因为AC⊥BC ,所以B1C1⊥A1C1,所以B1C1⊥平面AC1 .从而平面AB1C1⊥平面AC1(2) 1:1;(3) 点E位于AB的中点时,能使DE∥平面AB1C1.
解析试题分析:(1)由于ABC-A1B1C1是直三棱柱,所以B1C1⊥CC1;
又因为AC⊥BC ,所以B1C1⊥A1C1,所以B1C1⊥平面AC1 .
由于B1C1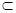 平面AB1C1,从而平面AB1C1⊥平面AC1 .
平面AB1C1,从而平面AB1C1⊥平面AC1 .
(2)由(1)知,B1C1⊥A1C .所以,若AB1⊥A1C,则可
得:A1C⊥平面AB1C1,从而A1C⊥ AC1 .
由于ACC1A1是矩形,故AC与AA1长度之比为1:1.
(3)点E位于AB的中点时,能使DE∥平面AB1C1.
证法一:设F是BB1的中点,连结DF、EF、DE.
则易证:平面DEF//平面AB1C1,从而
DE∥平面AB1C1.
证法二:设G是AB1的中点,连结EG,则易证EG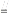 DC1.
DC1.
所以DE// C1G,DE∥平面AB1C1.
考点:线面平行垂直的判定及性质
点评:题目中涉及到中点D,要得到的关系恰好是线面平行,因此考虑由中点构成的三角形中位线从而实现线面平行关系

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 中,
中, 底面
底面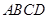 ,
,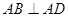 ,
,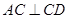 ,
,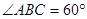 ,
,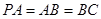 .
.
 平面
平面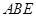 ;
;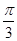 ,并说明理由.
,并说明理由.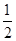 AD=1,CD=
AD=1,CD=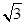 .
.
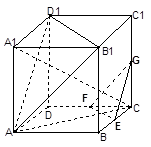
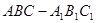 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,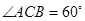 ,E、F分别是
,E、F分别是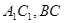 的中点。
的中点。
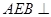 平面
平面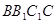 ;
;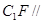 平面ABE;
平面ABE;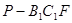 的体积。
的体积。 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形,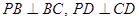 ,且
,且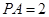 ,
,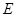 为
为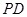 中点.
中点.
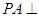 平面
平面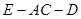 的余弦值.
的余弦值. 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
 //平面
//平面 ;
; ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
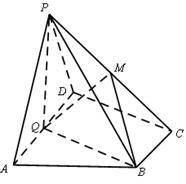
的值。 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD= .
.
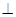 平面PBC;
平面PBC; ,当a为何值时,PC//平面
,当a为何值时,PC//平面 .
.