题目内容
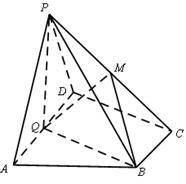
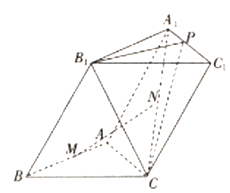
(本题满分16分)如图,在六面体 中,
中, ,
, ,
, .
.
求证:(1) ;(2)
;(2) .
.
(1)取线段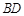 的中点
的中点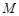 ,连结
,连结 、
、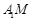 ,因为
,因为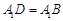 ,
,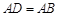
所以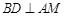 ,
,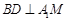 又
又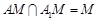 ,
,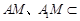 平面
平面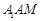 ,所以
,所以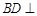 平面
平面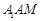 .而
.而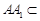 平面
平面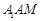 ,所以
,所以 .
.
(2)因为 ,
,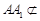 平面
平面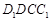 ,
,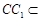 平面
平面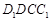 ,所以
,所以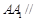 平面
平面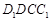 .
.
又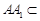 平面
平面 ,平面
,平面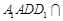 平面
平面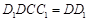 ,所以
,所以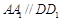 .同理得
.同理得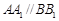 ,所以
,所以
解析试题分析:(1)取线段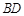 的中点
的中点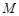 ,连结
,连结 、
、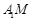 ,因为
,因为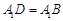 ,
,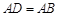
所以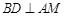 ,
,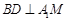 又
又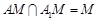 ,
,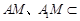 平面
平面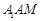 ,所以
,所以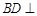 平面
平面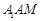 .而
.而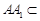 平面
平面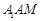 ,所以
,所以 .
.
(2)因为 ,
,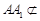 平面
平面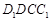 ,
,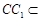 平面
平面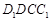 ,所以
,所以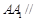 平面
平面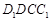 .
.
又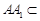 平面
平面 ,平面
,平面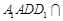 平面
平面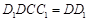 ,所以
,所以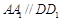 .同理得
.同理得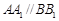 ,所以
,所以
考点:本题考查了空间中的线面关系
点评:高考中的立体几何问题主要是探求和证明空间几何体中的平行和垂直关系以及空间角、体积等计算问题.对于平行和垂直问题的证明或探求,其关键是把线线、线面、面面之间的关系进行灵活的转化

练习册系列答案
相关题目
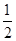 AD=1,CD=
AD=1,CD=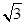 .
.
 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形,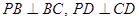 ,且
,且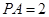 ,
,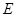 为
为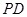 中点.
中点.
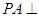 平面
平面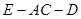 的余弦值.
的余弦值. 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
 //平面
//平面 ;
; ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
的值。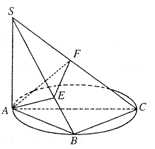
 求三棱锥S—AEF的体积.
求三棱锥S—AEF的体积. 中,
中,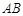 ∥
∥ ,
, ,
, ,
,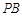 ⊥
⊥ ,
, ⊥
⊥ 为
为 的中点.
的中点.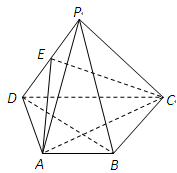
 ∥平面
∥平面 ;
; .
.
 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD= .
.
 平面PBC;
平面PBC; ,当a为何值时,PC//平面
,当a为何值时,PC//平面 .
. ,底面
,底面 是正方形,
是正方形, 面
面 是
是 的中点,点
的中点,点 是
是 的中点,连接
的中点,连接 ,
,
 .
.
 面
面 ;
; ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.