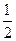题目内容
在R上定义运算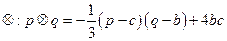 (b、c为实常数)。记
(b、c为实常数)。记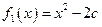 ,
,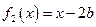 ,
,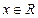 。令
。令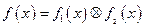 。
。
(Ⅰ)如果函数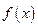 在
在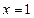 处有极值
处有极值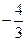 ,试确定b、c的值;
,试确定b、c的值;
(Ⅱ)求曲线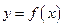 上斜率为c的切线与该曲线的公共点;
上斜率为c的切线与该曲线的公共点;
(Ⅲ)记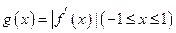 的最大值为
的最大值为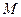 ,若
,若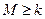 对任意的b、c恒成立,试示
对任意的b、c恒成立,试示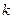 的最大值。
的最大值。
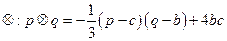 (b、c为实常数)。记
(b、c为实常数)。记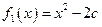 ,
,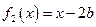 ,
,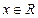 。令
。令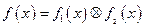 。
。(Ⅰ)如果函数
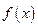 在
在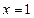 处有极值
处有极值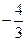 ,试确定b、c的值;
,试确定b、c的值;(Ⅱ)求曲线
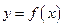 上斜率为c的切线与该曲线的公共点;
上斜率为c的切线与该曲线的公共点;(Ⅲ)记
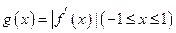 的最大值为
的最大值为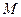 ,若
,若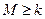 对任意的b、c恒成立,试示
对任意的b、c恒成立,试示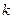 的最大值。
的最大值。(Ⅰ)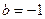 ,
,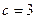
(Ⅱ)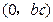 ,
,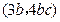 或
或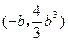 ,
,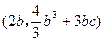
(Ⅲ)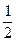
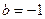 ,
,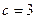
(Ⅱ)
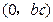 ,
,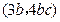 或
或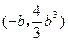 ,
,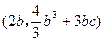
(Ⅲ)
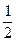
由R上运算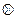 的定义及函数
的定义及函数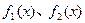 的表达式,
的表达式,
可得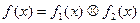
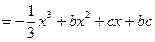 ∴
∴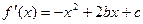 。
。
(Ⅰ)∵函数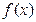 在
在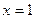 处有极值
处有极值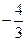 ,∴
,∴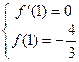 ,
,
得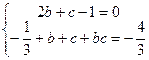 ,
,
从而解得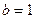 ,
,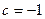 或
或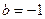 ,
,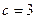
但当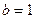 ,
,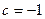 时,
时,
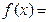
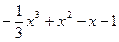 ,
,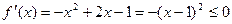 恒成立,
恒成立,
从而当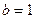 ,
,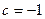 时,
时,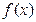 单调递减,故
单调递减,故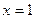 不是极值点而是拐点。
不是极值点而是拐点。
所以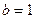 ,
,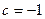 要舍去。
要舍去。
当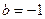 ,
,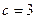 时,则
时,则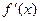
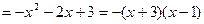 。当
。当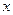 变化时,
变化时,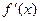 、
、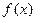 的变化情况如下表:
的变化情况如下表:
∴当x=1时,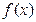 在有极大值
在有极大值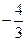 。因此
。因此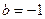 ,
,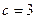 。
。
(Ⅱ)设x0是曲线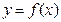 上的斜率为c的切线与曲线的切点,则
上的斜率为c的切线与曲线的切点,则
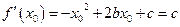 ,得x0=0或x0=2b,当x0=0时
,得x0=0或x0=2b,当x0=0时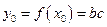 ;
;
当x0=2b时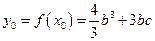 ,故切线的方程为
,故切线的方程为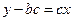
或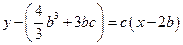 ,联立
,联立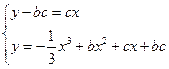
得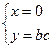 或
或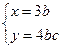
联立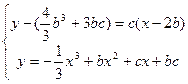 得
得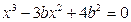 ,
,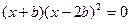 ,
,
解得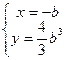 或
或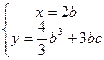
综上所述,曲线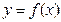 上斜率为c的切线与该曲线的公共点为
上斜率为c的切线与该曲线的公共点为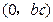 ,
,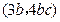
或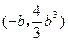 ,
,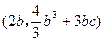 。
。
(Ⅲ)记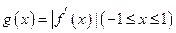 ,
,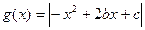 (
(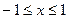 ),
),
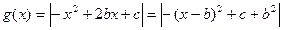 (
(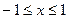 ),
),
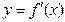 的对称轴为
的对称轴为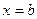
(1)当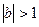 时,
时,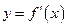 ,对称轴:x=b在区间
,对称轴:x=b在区间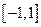 外面,从而
外面,从而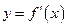 在
在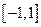
上的最大值在区间端点处取得。
记g(1),g(-1)中的最大者为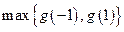 ,则
,则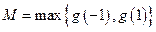 ,
,
所以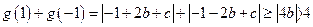 ,而
,而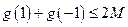 ,故当
,故当
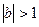 时M>2。
时M>2。
(2)当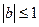 时,
时,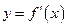 ,区间
,区间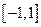 跨越对称轴:x=b,
跨越对称轴:x=b,
从而此时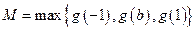 ,
,
因为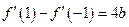 ,所以
,所以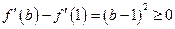 ,
,
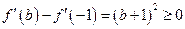 。
。
①当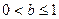 时,
时,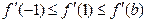 ,所以
,所以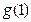
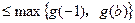 ,因此
,因此
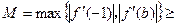
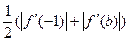
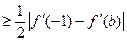
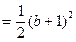
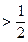
②当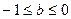 时,
时,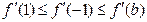 ,所以
,所以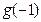
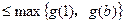 ,因此
,因此
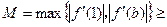
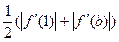
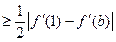
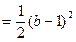
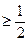
综上所述,对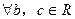 ,都有
,都有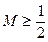 成立。
成立。
故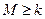 对任意的b、c恒成立的
对任意的b、c恒成立的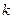 的最大值为
的最大值为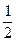 。
。
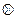 的定义及函数
的定义及函数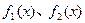 的表达式,
的表达式,可得
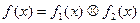
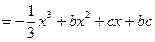 ∴
∴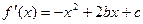 。
。(Ⅰ)∵函数
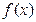 在
在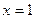 处有极值
处有极值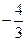 ,∴
,∴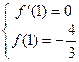 ,
,得
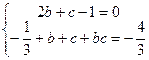 ,
,从而解得
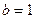 ,
,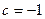 或
或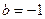 ,
,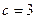
但当
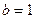 ,
,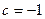 时,
时,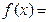
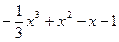 ,
,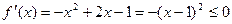 恒成立,
恒成立,从而当
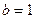 ,
,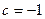 时,
时,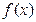 单调递减,故
单调递减,故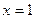 不是极值点而是拐点。
不是极值点而是拐点。所以
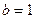 ,
,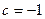 要舍去。
要舍去。当
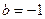 ,
,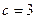 时,则
时,则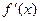
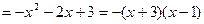 。当
。当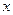 变化时,
变化时,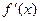 、
、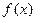 的变化情况如下表:
的变化情况如下表: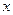 | 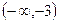 | 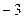 | 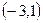 | 1 | 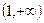 |
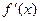 | ﹣ | 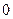 | ﹢ | 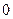 | ﹣ |
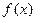 | ↘ | 极小值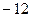 | ↗ | 极大值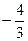 | ↘ |
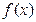 在有极大值
在有极大值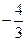 。因此
。因此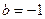 ,
,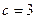 。
。(Ⅱ)设x0是曲线
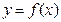 上的斜率为c的切线与曲线的切点,则
上的斜率为c的切线与曲线的切点,则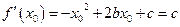 ,得x0=0或x0=2b,当x0=0时
,得x0=0或x0=2b,当x0=0时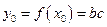 ;
;当x0=2b时
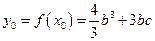 ,故切线的方程为
,故切线的方程为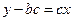
或
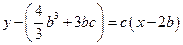 ,联立
,联立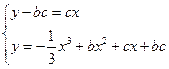
得
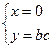 或
或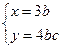
联立
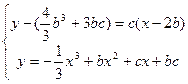 得
得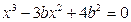 ,
,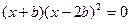 ,
,解得
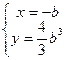 或
或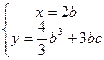
综上所述,曲线
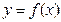 上斜率为c的切线与该曲线的公共点为
上斜率为c的切线与该曲线的公共点为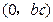 ,
,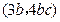
或
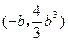 ,
,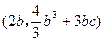 。
。(Ⅲ)记
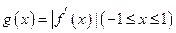 ,
,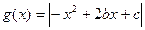 (
(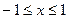 ),
),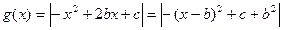 (
(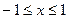 ),
),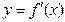 的对称轴为
的对称轴为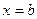
(1)当
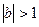 时,
时,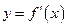 ,对称轴:x=b在区间
,对称轴:x=b在区间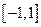 外面,从而
外面,从而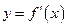 在
在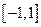
上的最大值在区间端点处取得。
记g(1),g(-1)中的最大者为
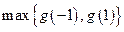 ,则
,则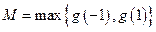 ,
,所以
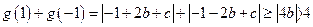 ,而
,而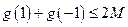 ,故当
,故当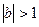 时M>2。
时M>2。(2)当
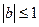 时,
时,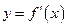 ,区间
,区间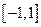 跨越对称轴:x=b,
跨越对称轴:x=b,从而此时
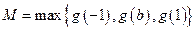 ,
,因为
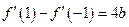 ,所以
,所以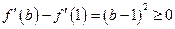 ,
,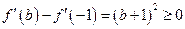 。
。①当
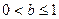 时,
时,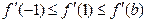 ,所以
,所以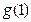
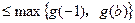 ,因此
,因此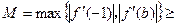
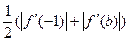
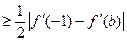
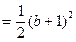
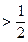
②当
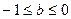 时,
时,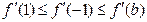 ,所以
,所以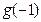
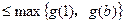 ,因此
,因此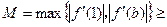
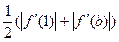
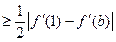
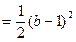
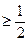
综上所述,对
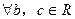 ,都有
,都有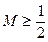 成立。
成立。故
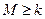 对任意的b、c恒成立的
对任意的b、c恒成立的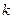 的最大值为
的最大值为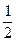 。
。
练习册系列答案
相关题目
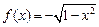 在区间
在区间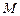 上的反函数是其本身,则
上的反函数是其本身,则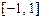

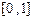
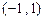

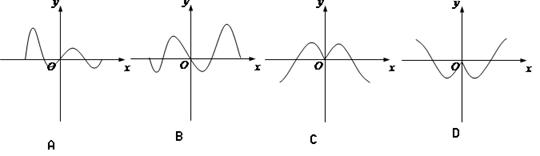
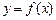 的图像如图2所示,那么导函数
的图像如图2所示,那么导函数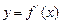 的图像可能是( )
的图像可能是( )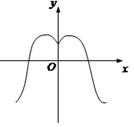
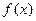 是定义在
是定义在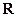 上的奇函数,且当
上的奇函数,且当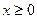 时,
时,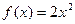 .
.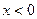 时,
时,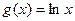 ,问是否存在
,问是否存在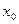 ,使得
,使得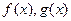 在x = x0处的切线互相平行?若存在,请求出
在x = x0处的切线互相平行?若存在,请求出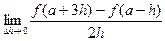 ; (2)
; (2)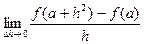
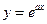 在点
在点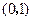 处的切线与直线
处的切线与直线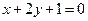 垂直,则
垂直,则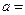 。
。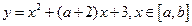 的图像关于直线
的图像关于直线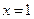 对称,则
对称,则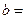 ________
________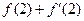 的值是 ( )
的值是 ( )