题目内容
1．化简：（1）$\frac{\sqrt{1+2sin20°cos20°}}{sin20°+\sqrt{1-si{n}^{2}20°}}$
（2）$\frac{\sqrt{1+2sin20°cos160°}}{sin160°-\sqrt{1-si{n}^{2}20°}}$．
分析 （1）由条件利用同角三角函数的基本关系求得所给式子的值．
（2）由条件利用同角三角函数的基本关系、诱导公式化简所给的式子，可得结果．
解答 解：（1）$\frac{\sqrt{1+2sin20°cos20°}}{sin20°+\sqrt{1-si{n}^{2}20°}}$=$\frac{\sqrt{{（cos20°+sin20°）}^{2}}}{sin20°+cos20°}$=$\frac{cos20°+sin20°}{sin20°+cos20°}$=1．
（2）$\frac{\sqrt{1+2sin20°cos160°}}{sin160°-\sqrt{1-si{n}^{2}20°}}$=$\frac{\sqrt{1-2sin20°cos20°}}{sin20°-cos20°}$=$\frac{\sqrt{{（cos20°-sin20°）}^{2}}}{sin20°-cos20°}$=$\frac{cos20°-sin20°}{sin20°-cos20°}$=-1．
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用，属于基础题．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
12．已知两座灯塔A、B与灯塔C的距离分别为1km，2km．灯塔A在C的北偏东20°，灯塔B在C的南偏东40°，则灯塔A与B的距离为（ ）km．
| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{6}$ | D． | $\sqrt{7}$ |
9．电灯泡使用时间在1000小时以上概率为0.2，则3个灯泡在使用1000小时后坏了1个的概率是（ ）
| A． | 0.128 | B． | 0.096 | C． | 0.104 | D． | 0.384 |
13．若某几何体的三视图 （单位：cm） 如图所示，则此几何体的表面积是（cm2）（ ）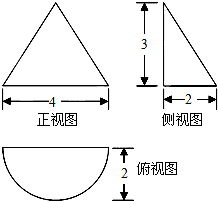
| A． | 2$\sqrt{13}$π+6 | B． | 2π+6 | C． | $6+（2\sqrt{13}+2）π$ | D． | $6+（\sqrt{13}+2）π$ |
已知函数f（x）=$\sqrt{3}sin2x-2{sin^2}$x+2，x∈R