题目内容
12．已知两座灯塔A、B与灯塔C的距离分别为1km，2km．灯塔A在C的北偏东20°，灯塔B在C的南偏东40°，则灯塔A与B的距离为（ ）km．| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{6}$ | D． | $\sqrt{7}$ |
分析 先根据题意求得∠ACB，进而根据余弦定理求得AB．
解答 
解：依题意知∠ACB=180°-20°-40°=120°，
在△ABC中，由余弦定理知AB=$\sqrt{1+4-2×1×2×cos120°}$=$\sqrt{7}$．
即灯塔A与灯塔B的距离为$\sqrt{7}$km．
故选：D．
点评 本题主要考查余弦定理的应用．正弦定理和余弦定理在解三角形和解决实际问题时用的比较多，这两个定理及其推论，一定要熟练掌握并要求能够灵活应用．
练习册系列答案
快捷英语周周练系列答案
相关题目
20．下列关于函数f（x）=-2sin2x-cos4x（x∈R）的说法正确的是（ ）
| A． | f（x）的最小正周期为2π | B． | f（x）的最大值为-1 | ||
| C． | f（x）是偶函数 | D． | f（x）在[$\frac{π}{12}$，$\frac{π}{4}$]上单调增 |
17．“sinA=$\frac{1}{2}$”是“A=30°”的（ ）
| A． | 充分而不必要条件 | B． | 既不充分也不必要条件 | ||
| C． | 充分必要条件 | D． | 必要而不充分条件 |
4．sin（-60°）的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |
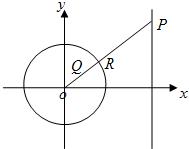已知圆C：x2+y2=4，直线l：x=8，以原点O为极点，x轴非负半轴为极轴建立极坐标系．