题目内容
6.设a为实数,0<a<1,函数f(x)在0≤x≤y≤1时,有f(0)=0,f(1)=1,f($\frac{x+y}{2}$)=(1-a)f(x)+af(y)(1)求a的值;
(2)求f($\frac{1}{7}$)的值.
分析 (1)f($\frac{x+y}{2}$)=(1-a)f(x)+af(y)进行赋值,可得出关于a的方程,即可求得a的值,
(2)由(1)可归纳得到f(x)=x,于是可以求出f($\frac{1}{7}$)的值.
解答 解:(1)由f($\frac{x+y}{2}$)=(1-a)f(x)+af(y),
令x=0,y=1,可得f($\frac{1}{2}$)=(1-a)f(0)+af(1)=a,
令x=0,y=$\frac{1}{2}$,可得f($\frac{1}{4}$)=(1-a)f(0)+af($\frac{1}{2}$)=a2,
令x=$\frac{1}{2}$,y=1,可得f($\frac{3}{4}$)=(1-a)f($\frac{1}{2}$)+af(1)=2a-a2,
令x=$\frac{1}{4}$,y=$\frac{3}{4}$,可得f($\frac{1}{2}$)=(1-a)f($\frac{1}{4}$)+af($\frac{3}{4}$),
∴a=(1-a)a2+a(2a-a2),
∴a(2a-1)(a-1)=0,
∵0<a<1,
∴a=$\frac{1}{2}$,
(2)由(1)可得,f(0)=0,f(1)=1,f($\frac{1}{2}$)=$\frac{1}{2}$,f($\frac{1}{4}$)=$\frac{1}{4}$,f($\frac{3}{4}$)=$\frac{3}{4}$,
∴可以猜测f(x)=x,
∴f($\frac{1}{7}$)=$\frac{1}{7}$.
点评 本题考查抽象函数,考查赋值法的运用,考查学生的计算能力,属于基础题

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
16.若某校研究性学习小组共6人,计划同时参观科普展,该科普展共有甲,乙,丙三个展厅,6人各自随机地确定参观顺序,在每个展厅参观一小时后去其他展厅,所有展厅参观结束后集合返回,设事件A为:在参观的第一小时时间内,甲,乙,丙三个展厅恰好分别有该小组的2个人;事件B为:在参观的第二个小时时间内,该小组在甲展厅人数恰好为2人.则P(B|A)=( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{16}$ |
17.“sinA=$\frac{1}{2}$”是“A=30°”的( )
| A. | 充分而不必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充分必要条件 | D. | 必要而不充分条件 |
11.已知m>0,则m+$\frac{16}{m}$取最小值时,当且仅当m=( )
| A. | 8 | B. | ±4 | C. | 4 | D. | 16 |
16.在等比数列3,6,12,…中,第5项为( )
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
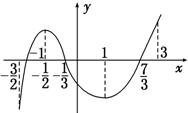 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].