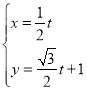题目内容
【题目】已知f(x)= ![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.f(x)为偶函数
B.f(x)为增函数
C.f(x)为周期函数
D.f(x)值域为(﹣1,+∞)
【答案】D
【解析】解:A.∵f(π)=π﹣1,f(﹣π)=sin2π=0,
∴f(﹣x)≠f(x),则函数f(x)不是偶函数,故A错误,
B.当x≤0时,函数不单调,则函数f(x)不是增函数,故B错误,
C.当x>0时,函数为增函数,不是周期函数,故C错误,
D.当x>0时,f(x)=|x|﹣1>﹣1,
当x≤0时,f(x)=sin2x∈[0,1],
综上f(x)>﹣1,即函数的值域为(﹣1,+∞),
故选:D
【考点精析】掌握命题的真假判断与应用和函数单调性的判断方法是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.

练习册系列答案
相关题目