题目内容
【题目】正项数列{an}的前n项和为Sn , 且2Sn=an2+an(n∈N*),设cn=(﹣1)n ![]() ,则数列{cn}的前2017项的和为 .
,则数列{cn}的前2017项的和为 .
【答案】- ![]()
【解析】解:当n=1时,2a1=a12+a1 , ∴a1=1或a1=0(舍).
当n≥2时,2an=2Sn﹣2Sn﹣1=an2+an﹣an﹣12﹣an﹣1 ,
∴an+an﹣1= ![]() 2﹣an﹣12=(an+an﹣1)(an﹣an﹣1).
2﹣an﹣12=(an+an﹣1)(an﹣an﹣1).
∵an+an﹣1≠0,∴an﹣an﹣1=1,
∴{an}是以1为首项,以1为公差的等差数列.
∴an=n,2Sn=n2+n.
∴cn=(﹣1)n ![]() =(﹣1)n(
=(﹣1)n( ![]() ).
).
设cn的前n项和为Tn ,
则T2017=﹣1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…﹣
+…﹣ ![]() ﹣
﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() =﹣
=﹣ ![]() .
.
所以答案是:- ![]() .
.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系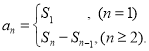 .
.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目