题目内容
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
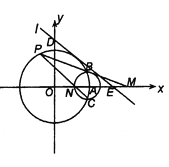
(2)设点![]() 在
在![]() 轴上的射影为点
轴上的射影为点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)本问考查求椭圆标准方程,根据点![]() 在椭圆上,代入得
在椭圆上,代入得![]() ,又离心率
,又离心率![]() ,于是可以求出
,于是可以求出![]() 的值,得到椭圆标准方程;(Ⅱ)点
的值,得到椭圆标准方程;(Ⅱ)点![]() 在
在![]() 轴上的射影
轴上的射影![]() 的坐标为
的坐标为![]() ,过点N的直线
,过点N的直线![]() 分两种情况进行讨论,当斜率为0时,经分析,不满足
分两种情况进行讨论,当斜率为0时,经分析,不满足![]() ,当
,当![]() 的斜率不为0时,可设方程为
的斜率不为0时,可设方程为![]() ,与椭圆方程联立,消元,得到关于
,与椭圆方程联立,消元,得到关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,于是可以根据前面的关系式求出
,于是可以根据前面的关系式求出![]() 的值,得到直线方程.
的值,得到直线方程.
试题解析:(Ⅰ)由已知可得![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,
,
所以椭圆Γ的方程为![]() .
.
(Ⅱ)由已知N的坐标为![]() ,
,
当直线![]() 斜率为0时,直线
斜率为0时,直线![]() 为
为![]() 轴,易知
轴,易知![]() 不成立.
不成立.
当直线![]() 斜率不为0时,设直线
斜率不为0时,设直线![]() 的方程为
的方程为![]() ,
,
代入![]() ,整理得,
,整理得, ![]() ,
,
设![]() ,
, ![]() 则
则
![]() ,①
,① ![]() ,②
,②
由![]() ,得
,得![]() ,③
,③
由①②③解得![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】(本小题满分12分)某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
喜欢 | 不喜欢 | 合计 | |
大于40岁 | 20 | 5 | 25 |
20岁至40岁 | 10 | 20 | 30 |
合计 | 30 | 25 | 55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)