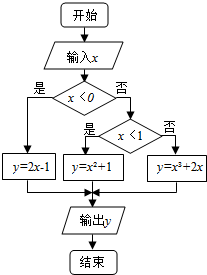
题目内容
11.椭圆$\frac{x^2}{2}$+y2=1的离心率是( )| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由椭圆方程可得a=$\sqrt{2}$,c=$\sqrt{2-1}$=1,从而求椭圆的离心率即可.
解答 解:∵椭圆方程为$\frac{x^2}{2}$+y2=1,
∴a=$\sqrt{2}$,c=$\sqrt{2-1}$=1,
故椭圆$\frac{x^2}{2}$+y2=1的离心率e=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故选:B.
点评 本题考查了椭圆的定义及离心率的求法,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.已知函数f(x)=m•9x-3x,若存在非零实数x0,使得f(-x0)=f(x0)成立,则实数m的取值范围是( )
| A. | m≥$\frac{1}{2}$ | B. | m≥2 | C. | 0<m<2 | D. | 0<m<$\frac{1}{2}$ |
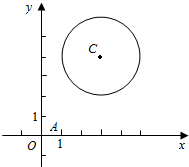 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).