题目内容
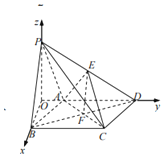
【题目】如图,在四棱锥P-ABCD中,底而ABCD是菱形,且PA=AD=2,∠PAD=∠BAD=120°,E,F分别为PD,BD的中点,且![]() .
.
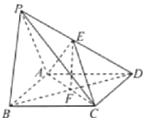
(1)求证:平面PAD⊥平面ABCD;
(2)求锐二面角E-AC-D的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先过P作PO⊥AD,再通过平几知识计算得PO⊥BO,利用线面垂直判定定理得PO⊥平面ABCD,再根据面面垂直判定定理得结果,(2)先根据条件建立空间直角坐标系,设立各点坐标,列方程组解得平面ACE的一个法向量,根据向量数量积得向量夹角,最后根据二面角与向量夹角关系得结果.
(1)过P作PO⊥AD,垂足为O,连结AO,BO,
由∠PAD=120°,得∠PAO=60°,
∴在Rt△PAO中,PO=PAsin∠PAO=2sin60°=2×![]() =
=![]() ,
,
∵∠BAO=120°,∴∠BAO=60°,AO=AO,∴△PAO≌△BAO,∴BO=PO=![]() ,
,
∵E,F分别是PA,BD的中点,EF=![]() ,∴EF是△PBD的中位线,
,∴EF是△PBD的中位线,
∴PB=2EF=2×![]() =
=![]() ,
,
∴PB2=PO2+BO2,∴PO⊥BO,∵AD∩BO=O,∴PO⊥平面ABCD,
又PO平面PAD,∴平面PAD⊥平面ABCD.
(2)以O为原点,OB为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,
A(0,1,0),P(0,0,![]() ),B(
),B(![]() ,0,0),D(0,3,0),
,0,0),D(0,3,0),
∴E(0,![]() ),F(
),F(![]() ,
,![]() ),
),![]() =(0,
=(0,![]() ),
),![]() =(
=(![]() ,
,![]() ,0),
,0),
易得平面ABCD的一个法向量![]() =(0,0,1),
=(0,0,1),
设平面ACE的法向量![]() =(x,y,z),则
=(x,y,z),则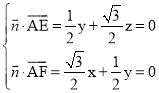 ,
,
取x=1,得![]() =(1,-
=(1,-![]() ,1),
,1),
设锐二面角的平面角的大小为θ,则cosθ=|cos<![]() >|=
>|=![]() =
=![]() ,
,
∴锐二面角E-AC-D的余弦值为![]() .
.

 优加精卷系列答案
优加精卷系列答案【题目】某企业购买某种仪器,在仪器使用期间可能出现故障,需要请销售仪器的企业派工程师进行维修,因为考虑到人力、成本等多方面的原因,销售仪器的企业提供以下购买仪器维修服务的条件:在购买仪器时,可以直接购买仪器维修服务,维修一次1000元;在仪器使用期间,如果维修服务次数不够再次购买,则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务,为此搜集并整理了500台这种机器在使用期内需要维修的次数,得到如下表格:
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数(台) | 50 | 100 | 150 | 100 | 100 |
记![]() 表示一台仪器使用期内维修的次数,
表示一台仪器使用期内维修的次数,![]() 表示一台仪器使用期内维修所需要的费用,
表示一台仪器使用期内维修所需要的费用,![]() 表示购买仪器的同时购买的维修服务的次数.
表示购买仪器的同时购买的维修服务的次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率,求![]() 的概率.
的概率.
(3)假设购买这500台仪器的同时每台都购买7次维修服务,或每台都购买8次维修服务,请分别计算这500台仪器在购买维修服务所需要费用的平均数,以此为决策依据,判断购买7次还是8次维修服务?