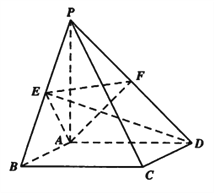
题目内容
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.

【答案】⑴![]() ⑵
⑵![]() ⑶圆过x轴上两个定点
⑶圆过x轴上两个定点![]() 和
和![]()
【解析】
⑴ 可得![]() ,从而
,从而![]() ,
,![]() ,即
,即![]()
⑵ 求得即![]() ,从而得
,从而得![]() ,
,![]() 代入双曲线方程知:
代入双曲线方程知: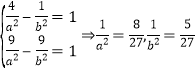 即可;
即可;
⑶ 可得![]() 的方程为:
的方程为:![]() ,求得
,求得![]() ,
,![]() ,
,
令![]() ,所以
,所以![]() ,
,
以MN为直径的圆的方程为:![]() ,
,
于是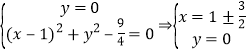 ,
,
即可得圆过x轴上两个定点.
解:⑴ 双曲线![]() 的渐近线方程为:
的渐近线方程为:
即![]() ,所以
,所以![]() ,
,
从而![]() ,
,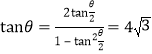 ,
,
所以![]()
⑵ 设![]() ,则由条件知:
,则由条件知:![]() ,
,![]() ,即
,即![]()
所以![]() ,
,![]() ,
,
代入双曲线方程知: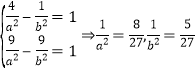
双曲线![]() 的方程:
的方程:![]()
⑶ 因为![]() ,所以
,所以![]() ,由⑴知,
,由⑴知,![]() ,所以
,所以![]() 的方程为:
的方程为:![]() ,
,
令![]() ,所以
,所以![]() ,
,![]() ,令
,令![]() ,所以
,所以![]() ,
,![]() ,令
,令![]() ,所以
,所以![]() ,
,
故以MN为直径的圆的方程为:![]() ,
,
即![]() ,
,
即![]() ,
,
若以MN为直径的圆恒经过定点![]()
于是
所以圆过x轴上两个定点![]() 和
和![]()

练习册系列答案
相关题目