题目内容
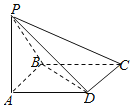
【题目】已知椭圆![]() 的两焦点分别为
的两焦点分别为![]() ,
,![]() ,
,![]() 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足![]() ,过
,过![]() 作倾斜角互补的两直线
作倾斜角互补的两直线![]() 、
、![]() 分别交椭圆于
分别交椭圆于![]() 、
、![]() 两点.
两点.
(1)求![]() 点坐标;
点坐标;
(2)当直线![]() 经过点
经过点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证直线![]() 的斜率为定值.
的斜率为定值.
【答案】(1)![]() (2)
(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)设![]()
![]() ,由题意可知
,由题意可知![]() 与
与![]() ,联立求解即可.
,联立求解即可.
(2)由题意可知,![]() 的斜率为-1,
的斜率为-1,![]() 的斜率为1,确定直线方程
的斜率为1,确定直线方程![]() 与直线
与直线![]() 的方程,然后分别与椭圆
的方程,然后分别与椭圆![]() 联立,求解
联立,求解![]() ,
,![]() 两点坐标,即可.
两点坐标,即可.
(3)由题意可知,直线![]() 、
、![]() 的斜率必存在,设
的斜率必存在,设![]() 的方程为:
的方程为:![]()
![]() ,与椭圆
,与椭圆![]() 联立,求解点
联立,求解点![]() 坐标,同理求解点
坐标,同理求解点![]() 坐标,求直线
坐标,求直线![]() 的斜率,即可.
的斜率,即可.
(1)由题可得![]() ,
,![]() ,
,
设![]()
![]()
则![]() ,
,![]() .
.
∴![]() 即
即![]()
∵点![]() 在曲线上,则
在曲线上,则![]() .
.
![]() 解得点
解得点![]() 的坐标为
的坐标为![]() .
.
(2)当直线![]() 经过点
经过点![]() 时,则
时,则![]() 的斜率为-1,
的斜率为-1,
因两条直线![]() 、
、![]() 的倾斜角互补,故
的倾斜角互补,故![]() 的斜率为1,
的斜率为1,
由
![]() 得,
得,![]() ,
,![]()
即![]() ,故
,故![]() ,
,
同理得![]() ,
,![]()
∴直线![]() 的方程为
的方程为![]()
(3)依题意,直线![]() 、
、![]() 的斜率必存在,不妨设
的斜率必存在,不妨设![]() 的方程为:
的方程为:![]()
![]() .
.
由 得
得![]() ,
,
设![]() ,则
,则 ,
,![]() ,
,
同理![]() ,则
,则![]() ,
,
同理![]() .
.
所以,![]() 的斜率
的斜率 为定值.
为定值.

练习册系列答案
相关题目
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式: 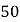 ,
, ![]() .
.
参考数据: ![]() .
.