题目内容
已知过抛物线y2 =2px(p>0)的焦点F的直线x-my+m=0与抛物线交于A,B两点,且△OAB(O为坐标原点)的面积为2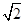 ,则m6+ m4的值为( )
,则m6+ m4的值为( )
| A.1 | B. 2 | C.3 | D.4 |
B
解析试题分析:由题意,可知该抛物线的焦点为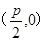 ,它过直线,代入直线方程,可知:
,它过直线,代入直线方程,可知: 求得
求得
∴直线方程变为:
A,B两点是直线与抛物线的交点,
∴它们的坐标都满足这两个方程.
∴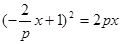
∴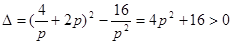
∴方程的解 ,
, ;
;
代入直线方程,可知: ,
, ,
,
△OAB的面积可分为△OAP与△OBP的面积之和,
而△OAP与△OBP若以OP为公共底,
则其高即为A,B两点的y轴坐标的绝对值,
∴△OAP与△OBP的面积之和为:
求得p=2,
∵ ,所以
,所以 ,∴
,∴ .
.
故答案为:B
考点:椭圆的简单性质
点评:本题主要考查了椭圆的简单性质,直线,抛物线与椭圆的关系.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
设F为抛物线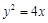 的焦点,
的焦点,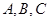 为抛物线上不同的三点,点
为抛物线上不同的三点,点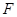 是△ABC的重心,
是△ABC的重心, 为坐标原点,△
为坐标原点,△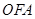 、△
、△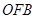 、△
、△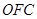 的面积分别为
的面积分别为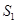 、
、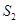 、
、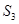 ,则
,则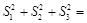 ( )
( )
| A.9 | B.6 | C.3 | D.2 |
已知点P是以F1、F2为焦点的椭圆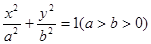 上一点,且
上一点,且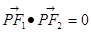 ,
,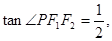 则该椭圆的离心率为( )
则该椭圆的离心率为( )
A.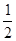 | B.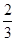 | C.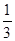 | D.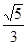 |
已知双曲线 :
:
 的离心率
的离心率 ,过双曲线
,过双曲线 的左焦点
的左焦点 作
作 :
: 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,则
,则 的大小等于( )
的大小等于( )
| A.45° | B.60° | C.90° | D.120° |
若方程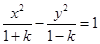 表示双曲线,则实数k的取值范围是 ( )
表示双曲线,则实数k的取值范围是 ( )
A. | B.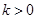 | C.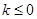 | D.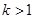 或 或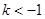 |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离为
到另一焦点距离为
A. | B. | C. | D. |
已知 是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引
是双曲线的两个焦点,Q是双曲线上任一点(不是顶点),从某一焦点引 的平分线的垂线,垂足为P,则点P的轨迹是
的平分线的垂线,垂足为P,则点P的轨迹是
| A.直线 | B.圆 | C.椭圆 | D.双曲线 |
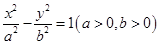 的两个焦点恰为椭圆
的两个焦点恰为椭圆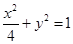 的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )
的两个顶点,且离心率为2,则该双曲线的标准方程为 ( )