题目内容
【题目】如图,矩形![]() 垂直于直角梯形
垂直于直角梯形![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() .
.
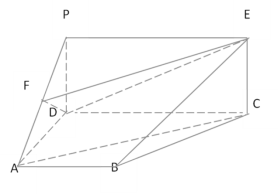
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在;![]()
【解析】
(1)连接PC,与DE交与点N,连接FN,可证出FN∥AC,再利用线面平行的判定定理即可证出.
(2)存在,Q为EF的中点,过F作FM⊥AD与M,连接MC,取MC的中点G,连接QG,由题中条件,求出![]() ,连接CQ,可得∠QCG为直线CQ与平面ABCD所成的角,在
,连接CQ,可得∠QCG为直线CQ与平面ABCD所成的角,在![]() 中,即可求解.
中,即可求解.
(1)连接PC,与DE交与点N,连接FN
在三角形PAC中,FN为中位线,所以FN∥AC,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以,AC∥平面DEF
(2)存在,Q为EF的中点.
过F作FM⊥AD与M,连接MC,取MC的中点G,连接QG
在三角形![]() 中,由条件可知,
中,由条件可知,![]() ,
,
在梯形![]() ,
,![]() 为中位线,所以
为中位线,所以![]()
连接CQ,则∠QCG为直线CQ与平面ABCD所成的角,
 ,所以存在点Q满足条件,
,所以存在点Q满足条件,
![]() .
.


练习册系列答案
相关题目
【题目】一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取![]() 名学生的数据如下表所示:
名学生的数据如下表所示:
满意 | 不满意 | 总计 | |
文科 | 22 | 18 | 40 |
理科 | 48 | 12 | 60 |
总计 | 70 | 30 | 100 |
(1)根据数据,有多大的把握认为对考试的结果满意与科别有关;
(2)用分层抽样方法在感觉不满意的学生中随机抽取![]() 名,理科生应抽取几人;
名,理科生应抽取几人;
(3)在(2)抽取的![]() 名学生中任取2名,求文科生人数的期望.(
名学生中任取2名,求文科生人数的期望.(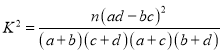 其中
其中![]() )
)
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |