题目内容
【题目】一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取![]() 名学生的数据如下表所示:
名学生的数据如下表所示:
满意 | 不满意 | 总计 | |
文科 | 22 | 18 | 40 |
理科 | 48 | 12 | 60 |
总计 | 70 | 30 | 100 |
(1)根据数据,有多大的把握认为对考试的结果满意与科别有关;
(2)用分层抽样方法在感觉不满意的学生中随机抽取![]() 名,理科生应抽取几人;
名,理科生应抽取几人;
(3)在(2)抽取的![]() 名学生中任取2名,求文科生人数的期望.(
名学生中任取2名,求文科生人数的期望.(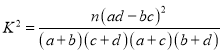 其中
其中![]() )
)
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(1)有![]() 的把握认为对考试的结果满意与科别无关(2)
的把握认为对考试的结果满意与科别无关(2)![]() 人(3)
人(3)![]()
【解析】
(1)利用独立性检验判断有多大的把握认为对考试的结果满意与科别有关;
(2)求出抽取的比例即得理科生应抽取的人数;
(3)设抽出的文科生的人数为![]() ,则
,则![]() ,再分别求出对应的概率,即得文科生人数的期望.
,再分别求出对应的概率,即得文科生人数的期望.
解:(1)由题意有:![]() ,所以有
,所以有![]() 的把握认为对考试的结果满意与科别无关.
的把握认为对考试的结果满意与科别无关.
(2)感觉不满意的学生共有![]() 人,抽取的比例为
人,抽取的比例为![]() ,所以理科生应抽取
,所以理科生应抽取![]() 人.
人.
(3)记抽取的![]() 名学生中,有
名学生中,有![]() 名文科生
名文科生![]() 名理科生,设抽出的文科生的人数为
名理科生,设抽出的文科生的人数为![]() ,
,
则![]() .
.
所以![]()
![]() .
.
所以![]() 的期望为
的期望为![]() .
.
所以抽出的文科生人数的期望为1.2.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目