Question

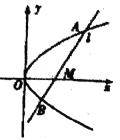
【题目】如图,曲线由曲线和曲线组成,其中点为曲线所在圆锥曲线的焦点,点为曲线所在圆锥曲线的焦点,

(1)若,求曲线的方程;

(2)如图,作直线平行于曲线的渐近线,交曲线于点,

求证:弦的中点必在曲线的另一条渐近线上;

(3)对于(1)中的曲线,若直线过点交曲线于点,求△面积的最大值．

Answer 1

【答案】（1）=和=；（2）见解析；（3）.

【解析】试题分析：本题主要考查椭圆与双曲线的方程与定义、直线与圆锥曲线的位置关系,考查了方程思想与弦长公式、逻辑推理能力与计算能力.(1)根据椭圆与双曲线的性质可得,求解可得曲线的方程;(2)由题意,设直线,与椭圆方程联立,利用根与系数的关系与中点坐标公式求出点M的坐标,则易得结论;(3)设直线的方程为,联立曲线C1的方程,利用根与系数的关系式,结合弦长公式与点到直线的距离公式求解.

试题解析：

(1)∵,

∴,

解得,

则曲线的方程为=和=.

(2)证明:曲线的渐近线为,

如图,设直线,

则,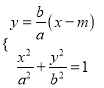

化为=,

,

解得．

又由数形结合知,

设点,

则= =,

∴===,

∴,

即点在直线上.

(3)由(1)知,曲线,点,

设直线的方程为,

联立方程组,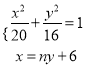

化为=,

,即,

设,

∴,

∴=,

===,

令,

∴,

∴===,

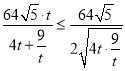当且仅当,即时等号成立,

∴时, =．