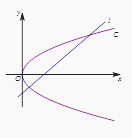
题目内容
【题目】设椭圆 ![]() 1(a>
1(a> ![]() )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 ![]() ,其中O为原点,e为椭圆的离心率.
,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若BF⊥HF,且∠MOA=∠MAO,求直线l的斜率.
【答案】
(1)
解:由 ![]() ,
,
得 ![]() +
+ ![]() =
= 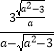 ,
,
即 ![]() =
= ![]() ,
,
∴a[a2﹣(a2﹣3)]=3a(a2﹣3),解得a=2.
∴椭圆方程为 ![]() ;
;
(2)
解:由已知设直线l的方程为y=k(x﹣2),(k≠0),
设B(x1,y1),M(x0,k(x0﹣2)),
∵∠MOA=∠MAO,
∴x0=1,
再设H(0,yH),
联立 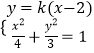 ,得(3+4k2)x2﹣16k2x+16k2﹣12=0.
,得(3+4k2)x2﹣16k2x+16k2﹣12=0.
△=(﹣16k2)2﹣4(3+4k2)(16k2﹣12)=144>0.
由根与系数的关系得 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
MH所在直线方程为y﹣k(x0﹣2)=﹣ ![]() (x﹣x0),
(x﹣x0),
令x=0,得yH=(k+ ![]() )x0﹣2k,
)x0﹣2k,
∵BF⊥HF,
∴ ![]() ,
,
即1﹣x1+y1yH=1﹣ ![]() [(k+
[(k+ ![]() )x0﹣2k]=0,
)x0﹣2k]=0,
整理得: ![]() =1,即8k2=3.
=1,即8k2=3.
∴k=﹣ ![]() 或k=
或k= ![]()
【解析】(1)由题意画出图形,把|OF|、|OA|、|FA|代入 ![]() +
+ ![]() =
= ![]() ,转化为关于a的方程,解方程求得a值,则椭圆方程可求;
,转化为关于a的方程,解方程求得a值,则椭圆方程可求;
(2)由已知设直线l的方程为y=k(x﹣2),(k≠0),联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求得B的坐标,再写出MH所在直线方程,求出H的坐标,由BF⊥HF,得 ![]() ,整理得到M的坐标与k的关系,由∠MOA=∠MAO,得到x0=1,转化为关于k的等式求得k的值.
,整理得到M的坐标与k的关系,由∠MOA=∠MAO,得到x0=1,转化为关于k的等式求得k的值.
本题考查椭圆方程的求法,考查直线与椭圆位置关系的应用,体现了“整体运算”思想方法和“设而不求”的解题思想方法,考查运算能力,是难题.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案