题目内容
9.已知函数f(x)=2x3-9x2+12x-5(1)求函数f(x)的单调区间;
(2)求函数f(x)的极值;
(3)求函数f(x)在区间[0,3]上的最值.
分析 (1)求出f(x)的导函数,运用导数的正负性求出单调区间;
(2)利用单调性求出极值,如果先增后减,有极大值;先减后增有极小值;
(3)求出区间端点值和极值,最大的即为函数的最大值,最小的即为函数的最小值.
解答 解;(1)定义域为R,
f′(x)=6x2-18x+12=6(x-1)(x-2)
当x∈(-∞,1)和(2,+∞)时,f′(x)>0,
当x∈(1,2)时,f′(x)<0
∴f(x)的单调增区间是(-∞,1)和(2,+∞),单调减区间为(1,2);
(2)由(1)知,当x=1时f(x)有极大值f(1)=0,当x=2时f(x)有极小值f(2)=-1;
(3)由(1)知f(x)在[0,1]上递增,在[1,2]上递减,在[2,3]上递增,
又f(0)=-5,f(3)=4结合(2)知
∴f(x)最大值为f(3)=4,最小值为f(0)=-5.
点评 本题考查了运用导数示函数的单调区间,极值和最值,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
9.甲、乙两人在2015年1月至5月的纯收入(单位:千元)的数据如下表:
(1)由表中数据直观分析,甲、乙两人中谁的纯收入较稳定?
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
10.设 Pn(xn,yn)是直线2x-y=$\frac{n}{n+1}$(n∈N*)与圆x2+y2=2在第一象限的交点,则极限$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
17.以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}x=3-t\\ y=t-5\end{array}\right.$(t为参数),圆C的极坐标方程为ρ=4(cosθ+sinθ),则圆C上的点到直线l的距离的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
1.给出下列两个推理:
①在△ABC中,若D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),由此推测:在空间四面体ABCD中,若M为△BCD的重心,则$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$).
②无根不循环小数都是无理数,因为e=2.7182818459045…是无限不循环小数,所以e是无理数.
对于上述两个推理,下列判断正确的是( )
①在△ABC中,若D为BC的中点,则$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),由此推测:在空间四面体ABCD中,若M为△BCD的重心,则$\overrightarrow{AM}$=$\frac{1}{3}$($\overrightarrow{AB}$+$\overrightarrow{AC}$+$\overrightarrow{AD}$).
②无根不循环小数都是无理数,因为e=2.7182818459045…是无限不循环小数,所以e是无理数.
对于上述两个推理,下列判断正确的是( )
| A. | ①是类比推理,②是归纳推理 | B. | ①是类比推理,②是演绎推理 | ||
| C. | ①是归纳推理,②是演绎推理 | D. | ①是演绎推理,②是类比推理 |
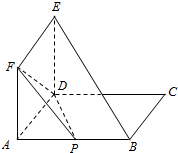 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.