题目内容

如图椭圆
x2
a2
+
y2
b2
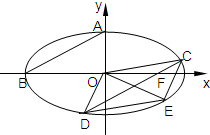
=1(a＞b＞0)的上顶点为A，左顶点为B，F为右焦点，过F作平行与AB的直线交椭圆于C、D两点．作平行四边形OCED，E恰在椭圆上．
（Ⅰ）求椭圆的离心率；
（Ⅱ）若平行四边形OCED的面积为
6
，求椭圆的方程．
（Ⅰ）∵焦点为F（c，0），AB斜率为
b
a
，故CD方程为y=
b
a
（x-c）．与椭圆联立后消去y得2x2-2cx-b2=0．
∵CD的中点为G（
c
2
，-
bc
2a
），点E（c，-
bc
a
）在椭圆上，
∴将E（c，-
bc
a
）代入椭圆方程并整理得2c2=a2，
∴e=
c
a
=
2
2
．
（Ⅱ）由（Ⅰ）知CD的方程为y=
2
2
（x-c），b=c，a=
2
c．
与椭圆联立消去y得2x2-2cx-c2=0．
∵平行四边形OCED的面积为：
S=c|yC-yD|=
2
2
c
(xC+xD)2-4xCxD

=
2
2
c
c2+2c2
=
6
2
c2=
6
，
∴c=
2
，a=2，b=
2
．
故椭圆方程为
x2
4
+
y2
2
=1．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
1
2
，F1、F2分别为椭圆C的左、右焦点，若椭圆C的焦距为2．
（1）求椭圆C的方程；
（2）设M为椭圆上任意一点，以M为圆心，MF1为半径作圆M，当圆M与直线l：x=
a2
c
有公共点时，求△MF1F2面积的最大值．
（2手11•浙江）设F1，F2分别为椭圆
x2
3
+y2=1的焦点，点A，B在椭圆上，若
F1A
=5
F2B
；则点A的坐标是______．
如图，A、B、C分别为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的顶点和焦点，若∠ABC=90°，则该椭圆的离心率为______．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)，左焦点为E，右焦点为F，上顶点为B，若△BEF为等边三角形，则此椭圆的离心率为（　　）
A．
5
+1
2
B．
5
-1
2
C．
1
2
D．2-
3
已知椭圆
x2
16
+
y2
9
=1的左、右焦点分别为F1、F2，过点F1的直线交椭圆于M、N两点，则△MNF2的周长为______．
已知△ABC为正三角形，点A，B为椭圆的焦点，点C为椭圆一顶点，则该三角形的面积与椭圆的四个顶点连成的菱形的面积之比为（　　）
A．
1
2
B．
1
4
C．
3
2
D．
3
3
椭圆
x2
2
+
y2
b2
=1的焦点为F1，F2，两条准线与x轴的交点分别为M，N，若|MN|≤2|F1F2|，则该椭圆离心率取得最小值时的椭圆方程为______．
设F1、F2是椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，P为直线x=-
3
2
a上一点，△F1PF2是底角为30°的等腰三角形，则E的离心率为（　　）
A．
1
2
B．
2
3
C．
3
4
D．
4
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网