题目内容

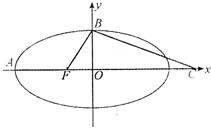
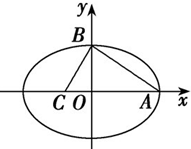
如图，A、B、C分别为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的顶点和焦点，若∠ABC=90°，则该椭圆的离心率为______．
∵Rt△ABC中，OC=c，OA=a，OB=b，且OB⊥AC
∴BO2=OC•OA，即b2=ac
结合b2=a2-c2，得a2-c2=ac，即c2+ac-a2=0
两边都除以a2，得e2+e-1=0，解之得e=
-1+
5
2
（舍负）
故答案为：
-1+
5
2
练习册系列答案
相关题目
如图，F是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的一个焦点，A、B是椭圆的两个顶点，椭圆的离心率为
1
2
，点C在x轴上，BC⊥BF，由B、C、F三点确定的圆M恰好与直线x+
3
y+3=0相切．
（I）求椭圆的方程；
（II）过F作一条与两坐标轴都不垂直的直线l交椭圆于P、Q两点，若在x轴上存在一点N（x0，0），使得直线NP与直线NQ关于x轴对称，求x0的值．
椭圆
x2
9
+
y2
16
=1的焦点坐标为（　　）
A．（0，5）和（0，-5）B．（5，0）和（-5，0）C．（0，
7
）和（0，-
7
）		D．（
7
，0）和（-
7
，0）
已知M是椭圆
x2
9
+
y2
5
=1上一点，F1，F2是椭圆的两个焦点，I是△MF1F2的内心，延长MI交F1F2于N，则
|MI|
|NI|
等于______．
如图，已知F1，F2是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为（　　）
A．
3
2
B．
5
3
C．
6
3
D．
2
5
5
已知椭圆
x2
4
+
y2
3
=1，左焦点为F，右顶点为C，过F作直线l与椭圆交于A，B两点，求△ABC面积最大值．
如图椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的上顶点为A，左顶点为B，F为右焦点，过F作平行与AB的直线交椭圆于C、D两点．作平行四边形OCED，E恰在椭圆上．
（Ⅰ）求椭圆的离心率；
（Ⅱ）若平行四边形OCED的面积为
6
，求椭圆的方程．
已知F1、F2是椭圆
x2
16
+
y2
25
=1的两个焦点，过F1的直线与椭圆交于M、N两点，则△MNF2的周长为______．
过椭圆
x2
36
+
y2
25
=1的焦点F1作直线l交椭圆于A、B两点，F2是此椭圆的另一个焦点，则△ABF2的周长为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网