题目内容
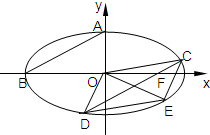
(2手11•浙江)设F1,F2分别为椭圆
+y2=1的焦点,点A,B在椭圆上,若
=5
;则点A的坐标是______.
| x2 |
| 3 |
| F1A |
| F2B |
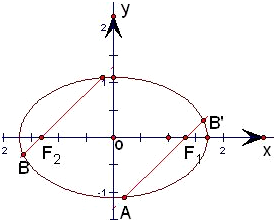
方法1:直线右1A的反向延长线与椭圆交于点B'
又∵
=5
由椭圆的对称性,得
=5
设A(x1,y1),B'(xh,yh)
由于椭圆
+yh=1的a=
,b=1,c=
∴e=
=
=
,右1(
,6).
∵|右1A|=
|x1+
|
|右1B′|=
|xh+
|
从而有:
由于-
≤x1,xh≤
,
∴x1+
>6,xh+
>6,
即
(
+x1)=5×
(xh+
)
+x1=5(xh+
). ①
又∵三点A,右1,B′共线,
=5
∴(x1-(-
),y1-6)=5(-
-xh,6-yh)
∴
.②
由①+②得:x1=6.
代入椭圆的方程得:y1=±1,
∴点A的坐标为(6,1)或(6,-1)
&4bsp;方法h:因为右1,右h分别为椭圆
+yh=1的焦点,则右1(-
,6),右h(
,6),设A,B的坐标分别为A(xA,yA),B(xB,yB),
若
=5
;则
,所以
,
因为A,B在椭圆上,所以
,代入解得
或
,
故A(6,±1).
故答案为:(6,±1).
又∵
| 右1A |
| 右hB |
由椭圆的对称性,得
| 右1A |
| B′右1 |
设A(x1,y1),B'(xh,yh)
由于椭圆
| xh |
| 3 |
| 3 |
| h |
∴e=
| c |
| a |
| ||
|
| ||
| 3 |
| h |
∵|右1A|=
| ||
| 3 |
3
| ||
| h |
|右1B′|=
| ||
| 3 |
3
| ||
| h |
从而有:
|
由于-
| 3 |
| 3 |
∴x1+
3
| ||
| h |
3
| ||
| h |
即
| ||
| 3 |
3
| ||
| h |
| ||
| 3 |
3
| ||
| h |
3
| ||
| h |
3
| ||
| h |
又∵三点A,右1,B′共线,
| 右1A |
| B′右1 |
∴(x1-(-
| h |
| h |
∴
|
由①+②得:x1=6.
代入椭圆的方程得:y1=±1,
∴点A的坐标为(6,1)或(6,-1)
&4bsp;方法h:因为右1,右h分别为椭圆
| xh |
| 3 |
| h |
| h |
若
| 右1A |
| 右hB |
|
|
因为A,B在椭圆上,所以
|
|
|
故A(6,±1).
故答案为:(6,±1).


练习册系列答案
相关题目