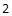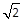题目内容

已知F1、F2是椭圆C：
x2
4
+y2=1的两个焦点，P为椭圆C在第一象限上的一点，且
PF1
⊥
PF2
．则P到x=
5
3
3
的距离为______．
∵椭圆C：
x2
4
+y2=1中，a2=4且b2=1，
∴c=
a2-b2
=
3
，可得焦点为F1（-
3
，0），F2（
3
，0）．
设P的坐标为（m，n），可得
PF1
=（-
3
-m，-n），
PF2
=（
3
-m，-n）．
∵
PF1
⊥
PF2
，∴
PF1
•
PF2
=（-
3
-m）（
3
-m）+n2=0，即m2+n2=3，…①
又∵点P在椭圆C上，∴
m2
4
+n2=1，…②
联解①②，得m=
2
3
3
、n=
3
3
（舍负），可得P的坐标为（
2
3
3
，
3
3
）．
因此点P到x=
5
3
3
的距离为|
5
3
3
-
2
3
3
|=
3
．
故答案为：
3
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F，C与过原点的直线相交于A，B两点，连接了AF，BF，若|AB|=10，|BF|=8，cos∠ABF=
4
5
，则C的离心率为（　　）
A．
3
5
B．
5
7
C．
4
5
D．
6
7
已知△ABC的顶点B，C在椭圆
x2
3
+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（　　）
A．2
3
B．6C．4
3
D．12
椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的两个焦点为F1（-c，0）、F2（c，0），M是椭圆上一点，且满足
F1M
•
F2M
=0．
（1）求离心率e的取值范围；
（2）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为5
2
，求此时椭圆的方程．
已知点A是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上一点，F为椭圆的一个焦点，且AF⊥x轴，|AF|=焦距，则椭圆的离心率是（　　）
A．
1+
5
2
B．
3
-1		C．
2
-1		D．
2
-
1
2
方程
x2
m2
+
y2
2+m
=1表示焦点在y轴上的椭圆，则m的范围是______．
已知椭圆的标准方程为
x2
6-m
+
y2
m-1
=1，
（1）若椭圆的焦点在x轴，求m的取值范围；
（2）试比较m=2与m=3时两个椭圆哪个更扁．
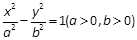已知双曲线与抛物线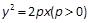有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若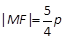, 则此双曲线的离心率等于(      )．
A．B．C．　　D．
椭圆
x2
25
+
y2
9
=1上一点M到左焦点F1的距离是4，M到右焦点F2的距离是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网