题目内容
2.已知点A(1,-1),B(5,-3),C(4,-5),则表示△ABC的边界及其内部的约束条件是$\left\{\begin{array}{l}{x+2y-1≥0}\\{2x-y-13≤0}\\{4x+3y-1≤0}\end{array}\right.$.分析 由点的坐标求出AB、BC、AC所在直线方程,然后借助于原点与直线的位置关系可得表示△ABC的边界及其内部的约束条件.
解答 解:由A(1,-1),B(5,-3),C(4,-5),
借助于直线方程的两点式求得:
AB:x+2y-1=0,
BC:2x-y-13=0,
AC:4x+3y-1=0.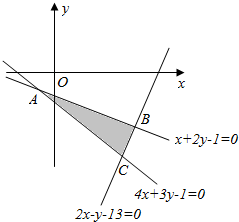
则表示△ABC的边界及其内部的约束条件是:$\left\{\begin{array}{l}{x+2y-1≥0}\\{2x-y-13≤0}\\{4x+3y-1≤0}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x+2y-1≥0}\\{2x-y-13≤0}\\{4x+3y-1≤0}\end{array}\right.$.
点评 本题考查简单的线性规划,考查了二元一次不等式组所表示的平面区域,是中档题.

练习册系列答案
相关题目
10.已知函数f(x)=sin2x-(2$\sqrt{2}+\sqrt{2}a$)sin(x+$\frac{π}{4}$)-$\frac{2\sqrt{2}}{cos(x-\frac{π}{4})}$,若对任意x∈[0,$\frac{π}{2}$],不等式f(x)>-3-2a恒成立,则实数a的取值范围是( )
| A. | a>2$\sqrt{2}$ | B. | a$<2\sqrt{2}$ | C. | a<3 | D. | a>3 |
14.复数z=$\frac{{{i^{2012}}}}{{{{(1-i)}^5}}}$的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知抛物线y2=8x焦点与双曲线$\frac{x^2}{a^2}-{y^2}=1$(a>0)的右焦点重合,则此双曲线的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
12.若x∈(1,e),a=ln x,b=(ln x)2,c=ln(ln x),则a,b,c的大小关系为( )
| A. | c>b>a | B. | b>c>a | C. | a>b>c | D. | b>a>c |