题目内容
10.已知函数f(x)=sin2x-(2$\sqrt{2}+\sqrt{2}a$)sin(x+$\frac{π}{4}$)-$\frac{2\sqrt{2}}{cos(x-\frac{π}{4})}$,若对任意x∈[0,$\frac{π}{2}$],不等式f(x)>-3-2a恒成立,则实数a的取值范围是( )| A. | a>2$\sqrt{2}$ | B. | a$<2\sqrt{2}$ | C. | a<3 | D. | a>3 |
分析 令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),把f(x)转化为t的函数g(t)=t2-(2+a)t-$\frac{4}{t}$-1,再由不等式f(x)>-3-2a恒成立,分离参数a后利用函数的单调性求得答案.
解答 解:∵x∈[0,$\frac{π}{2}$],
∴令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[1,$\sqrt{2}$],
∴t2=sin2x+cos2x+2sinxcosx,
则sinxcosx=$\frac{{t}^{2}-1}{2}$.
∴f(x)=2sinxcosx-(2+a)(sinx+cosx)-$\frac{4}{sinx+cosx}$.
∴f(x)=g(t)=t2-(2+a)t-$\frac{4}{t}$-1,t∈[1,$\sqrt{2}$].
∵函数f(x)>-3-2a恒成立,
∴t2-(2+a)t-$\frac{4}{t}$-1>-3-2a恒成立,
得:t2-2t-$\frac{4}{t}$+2>(t-2)a,
∵t-2<0,∴a>$\frac{{t}^{2}-2t}{t-2}$-$\frac{4-2t}{t(t-2)}$=t+$\frac{2}{t}$.
∵函数$y=t+\frac{2}{t}$在[1,$\sqrt{2}$]上是递减函数,
∴a>$(t+\frac{2}{t})_{max}$=3.
故选:D.
点评 本题考查函数恒成立问题,考查了三角函数中的恒等变换应用,训练了利用函数的单调性求函数的最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.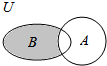 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )| A. | {x|-$\sqrt{3}≤x≤1$} | B. | {x|-3≤x≤1} | C. | {x|-3$≤x≤-\sqrt{3}$} | D. | {x|1$≤x≤\sqrt{3}$} |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1(a>$\sqrt{2}$)的两条渐近线的夹角为$\frac{π}{3}$,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |