题目内容
9.设A={-3,2a-1,a2+1},B={a-4,2-a,5}.(1)若0∈A,求A∩B;
(2)若A∩B={5},求A∪B.
分析 (1)若0∈A,求出a,即可求A∩B;
(2)若A∩B={5},建立方程关系即可求A∪B.
解答 解:(1)若0∈A,
则2a-1=0,则a=$\frac{1}{2}$,
即A={-3,0,1},B={-$\frac{7}{2}$,$\frac{3}{2}$,5},
则A∩B=∅;
(2)若A∩B={5},
则2a-1=5或a2+1=5,
即a=3或a=2或a=-2,
当a=3时,A={-3,5,10},B={-1,-1,5}.则集合B不成立,
当a=2时,A={-3,2,5},B={-2,0,5}.则A∪B={-3,0,2,5},
当a=-2时,A={-3,-5,5},B={-6,4,5}.则A∪B={-6,-5,-3,4,5}.
点评 本题主要考查集合的基本运算,根据集合元素关系求出a是解决本题的关键.注意要对a进行讨论.

练习册系列答案
相关题目
17.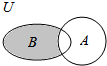 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )| A. | {x|-$\sqrt{3}≤x≤1$} | B. | {x|-3≤x≤1} | C. | {x|-3$≤x≤-\sqrt{3}$} | D. | {x|1$≤x≤\sqrt{3}$} |
3.若函数f(x)=$\left\{\begin{array}{l}{x+{3}^{x}(x≤0)}\\{\frac{1}{3}{x}^{3}-4x+a(x>0)}\end{array}\right.$在定义域上只有一个零点,则实数a的取值范围是( )
| A. | a>$\frac{16}{3}$ | B. | a<$\frac{16}{3}$ | C. | a≥$\frac{16}{3}$ | D. | a≤$\frac{16}{3}$ |