题目内容
8.设全集S={1,2,…,15},A={a1,a2,a3}是S的子集,且(a1,a2,a3)满足:1≤a1<a2<a3≤15,a3-a2≤6,求满足条件的子集的个数.分析 从集合S中任选3个元素组成集合A,一个能组成C153个,再把不符合条件的去掉,就得到满足条件的集合A的个数.
解答 解:从集合S中任选3个元素组成集合A,一共能组成C153=455个,
其中a3=8时,a1,a2∈{1,2}不满足要求,共有C22=1个,
a3=9时,a1,a2∈{1,2,3}不满足要求,共有C32=3个,
a3=10时,a1,a2∈{1,2,3,4}不满足要求,共有C42=6个,
a3=11时,a1,a2∈{1,2,3,4,5}不满足要求,共有C52=10个,
a3=12时,a1,a2∈{1,2,3,4,5,6}不满足要求,共有C62=15个,
a3=13时,a1,a2∈{1,2,3,4,5,6,7}不满足要求,共有C72=21个,
a3=14时,a1,a2∈{1,2,3,4,5,6,7,8}不满足要求,共有C82=28个,
a3=15时,a1,a2∈{1,2,3,4,5,6,7,8,9}不满足要求,共有C92=36个,
其它的都符合条件,
所以满足条件的集合A的个数455-(1+3+6+10+15+21+28+36)=345.
点评 本题主要考查排列与组合及两个基本原理,组合数公式的应用,元素与集合的关系,解题时要认真审题,仔细思考,认真解答,属于中档题.

练习册系列答案
相关题目
17.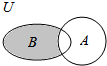 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )| A. | {x|-$\sqrt{3}≤x≤1$} | B. | {x|-3≤x≤1} | C. | {x|-3$≤x≤-\sqrt{3}$} | D. | {x|1$≤x≤\sqrt{3}$} |