题目内容
(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分.
设常数 ,函数
,函数
若 =4,求函数
=4,求函数 的反函数
的反函数 ;
;
根据 的不同取值,讨论函数
的不同取值,讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(1) ,
, ;(2)
;(2) 时
时 为奇函数,当
为奇函数,当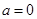 时
时 为偶函数,当
为偶函数,当 且
且 时
时 为非奇非偶函数.
为非奇非偶函数.
解析试题分析:(1)求反函数,就是把函数式 作为关于
作为关于 的方程,解出
的方程,解出 ,得
,得 ,再把此式中的
,再把此式中的 互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在
互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在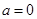 ,
, 这两种情况下,由奇偶性的定义可知函数
这两种情况下,由奇偶性的定义可知函数 具有奇偶性,在
具有奇偶性,在 时,函数的定义域是
时,函数的定义域是 ,不关于原点对称,因此函数既不是奇函数也不是偶函数.
,不关于原点对称,因此函数既不是奇函数也不是偶函数.
试题解析:(1)由 ,解得
,解得 ,从而
,从而 ,
,
∴ ,
,
∵ 且
且
∴①当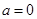 时,
时, ,
,
∴对任意的 都有
都有 ,∴
,∴ 为偶函数
为偶函数
②当 时,
时, ,
, ,
,
∴对任意的 且
且 都有
都有 ,∴
,∴ 为奇函数
为奇函数
③当 且
且 时,定义域为
时,定义域为 ,
,
∴定义域不关于原定对称,∴ 为非奇非偶函数
为非奇非偶函数
【考点】反函数,函数奇偶性.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 .
. 的定义域;
的定义域;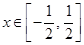 时,函数
时,函数 ,求函数
,求函数 的值域.
的值域. 上函数
上函数 为奇函数.
为奇函数. 的值;
的值; 的值域.
的值域. 上的奇函数
上的奇函数 ,当
,当 时,
时,
 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
 在区间
在区间 上单调递减,求
上单调递减,求 的取值范围;
的取值范围; 时,
时, 恒成立,求
恒成立,求 的最大值及此时
的最大值及此时 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
. 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围; 时函数
时函数 ;
; .令
.令 的值.
的值. .
. .
.