题目内容
已知定义在 上函数
上函数 为奇函数.
为奇函数.
(1)求 的值;
的值;
(2)求函数 的值域.
的值域.
(1) ;(2)函数
;(2)函数 的值域为
的值域为 .
.
解析试题分析:(1)根据函数 为定义在
为定义在 上的奇函数,得到关系式
上的奇函数,得到关系式 ,代入函数的解析式,从中求解方程组即可得出
,代入函数的解析式,从中求解方程组即可得出 的值,从而可计算出
的值,从而可计算出 的值;(2)因为
的值;(2)因为 的分子为一次式,分母为二次式,从而可利用判别式法或基本不等式法进行求解该函数的值域.
的分子为一次式,分母为二次式,从而可利用判别式法或基本不等式法进行求解该函数的值域.
试题解析:(1)因为 为
为 上的奇函数
上的奇函数
所以 即
即
所以
(2)法一:设 的值域为
的值域为
则 当且仅当关于
当且仅当关于 的方程
的方程 有根,当
有根,当 时,根为
时,根为 符合;
符合;
当 时,
时, ,于是
,于是 且
且 ;
;
综上可知,函数 的值域为
的值域为
法二:当 时,
时,
当 时,
时, (当且仅当
(当且仅当 时等号成立)
时等号成立)
所以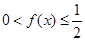
当 时,
时, 即
即 (当且仅当
(当且仅当 即
即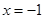 时等号成立)
时等号成立)
所以 ,所以
,所以
综上可知函数 的值域为
的值域为 .
.
考点:1.函数的奇偶性;2.函数值域的求法——判别式法、基本不等式法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
.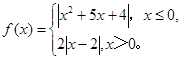 ,若函数
,若函数 恰有4个零点,则实数a的取值范围为 .
恰有4个零点,则实数a的取值范围为 . 在其定义域上为奇函数.
在其定义域上为奇函数.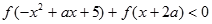 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 在定义域内恒成立;
在定义域内恒成立; 时,
时, 恒成立,求m的取值范围.
恒成立,求m的取值范围. ,函数
,函数
 =4,求函数
=4,求函数 的反函数
的反函数 ;
; ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 是函数
是函数 的导函数,求函数
的导函数,求函数 上的最小值;
上的最小值; ,函数
,函数 内有零点,求
内有零点,求 的取值范围
的取值范围
 的最小值;
的最小值;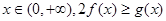 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的坐标分别为
的坐标分别为 .如果
.如果 是
是 围成的区域(含边界)上的点,那么当
围成的区域(含边界)上的点,那么当 取到最大值时,点
取到最大值时,点 的坐标是 .
的坐标是 .