题目内容
已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性;
的奇偶性;
(3)当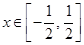 时,函数
时,函数 ,求函数
,求函数 的值域.
的值域.
(1)函数 的定义域为
的定义域为 ;(2)函数
;(2)函数 是奇函数;(3)函数
是奇函数;(3)函数 的值域为
的值域为 .
.
解析试题分析:(1)具有解析式的函数的定义域无特殊情况下,通常就是使解析式有意义的自变量的取值范围;通常关注的是:①开偶次方时被开方的式子为非负;②作为分母不得为零;③作为对数的真数必须为正;④作为对数的底数必须为正且不为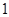 ;(2)奇、偶性的判断,首先必须关注定义域,定义域关于原点对称是函数具备奇、偶性的必要条件,接下来用定义或等价定义来判断;(3)求函数值域的方法很多,在大题中经常通过探讨函数单调性来达到求函数值域的目的,这里即是.
;(2)奇、偶性的判断,首先必须关注定义域,定义域关于原点对称是函数具备奇、偶性的必要条件,接下来用定义或等价定义来判断;(3)求函数值域的方法很多,在大题中经常通过探讨函数单调性来达到求函数值域的目的,这里即是.
试题解析:(1)由 得
得 ,则函数
,则函数 的定义域为
的定义域为 . 4分
. 4分
(2)当 时,
时,
 ,
,
因此,函数 是奇函数. 9分
是奇函数. 9分
(3)设 ,当
,当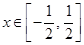 时,
时,
则函数 在区间
在区间 上是减函数,
上是减函数,
故函数 在区间
在区间 上也是减函数. 12分
上也是减函数. 12分
(证明单调性也可用定义)
则 ,
, 13分
13分
因此,函数 的值域为
的值域为 . 14分
. 14分
考点:函数的定义域、值域、单调性、奇偶性等的综合应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 .
.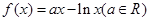 。
。 时,求曲线
时,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; 时,求
时,求 上的最小值。
上的最小值。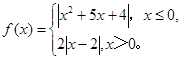 ,若函数
,若函数 恰有4个零点,则实数a的取值范围为 .
恰有4个零点,则实数a的取值范围为 . 在其定义域上为奇函数.
在其定义域上为奇函数.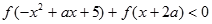 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,函数
,函数
 =4,求函数
=4,求函数 的反函数
的反函数 ;
; 的反函数是 .
的反函数是 . 是奇函数,则
是奇函数,则 .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m 
