题目内容
已知定义在 上的奇函数
上的奇函数 ,当
,当 时,
时,
(1)求函数 在
在 上的解析式;(2)若函数
上的解析式;(2)若函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
(1) (2)
(2)
解析试题分析:(1)因为x>0的解析式去为 所以可以求x<0的解析式
所以可以求x<0的解析式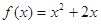 函数是奇函数所以f(0)=0综上所述
函数是奇函数所以f(0)=0综上所述 (2)要使f(x)在[-1,a-2]上单调递增.由图像可知
(2)要使f(x)在[-1,a-2]上单调递增.由图像可知 解得不等式为:
解得不等式为: .
.
试题解析:(1)设x<0,则-x>0,  . 3分
. 3分
又f(x)为奇函数,所以f(-x)=-f(x).
于是x<0时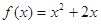 5分
5分
所以 6分
6分
(2)要使f(x)在[-1,a-2]上单调递增, (画出图象得2分)
结合f(x)的图象知  10分
10分
所以 故实数a的取值范围是(1,3]. 12分
故实数a的取值范围是(1,3]. 12分
考点:函数奇偶性,函数单调性.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 表示自然数
表示自然数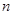 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9, ,10的因数有1,2,5,10,
,10的因数有1,2,5,10, ,那么
,那么
 ;
; .
.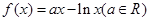 。
。 时,求曲线
时,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; 时,求
时,求 上的最小值。
上的最小值。 在其定义域上为奇函数.
在其定义域上为奇函数.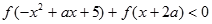 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 为常数,
为常数, ,函数
,函数 ,
, 且方程
且方程 有等根.
有等根. 的解析式及值域;
的解析式及值域; ,
, ,若
,若 ,求实数
,求实数 的取值范围;
的取值范围;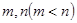 ,使
,使 的定义域和值域分别为
的定义域和值域分别为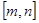 和
和 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. ,函数
,函数
 =4,求函数
=4,求函数 的反函数
的反函数 ;
;
 的简图;
的简图; 有三个不等实根,求k值的集合;
有三个不等实根,求k值的集合; 时,函数
时,函数 的下方,试求出k值的集合。
的下方,试求出k值的集合。 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).