题目内容
(本小题满分12分)
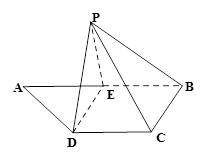
如图,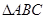 是直角三角形,
是直角三角形,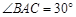 ,
,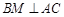 交
交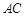 于点
于点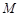 ,
,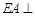 平面
平面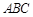 ,
,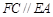 ,
,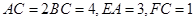 .
.
(1)证明: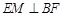 ;
;
(2)求平面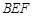 与平面
与平面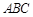 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.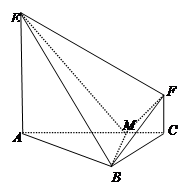
如图,
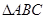 是直角三角形,
是直角三角形,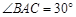 ,
,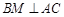 交
交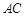 于点
于点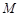 ,
,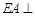 平面
平面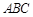 ,
,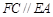 ,
,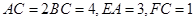 .
.(1)证明:
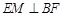 ;
;(2)求平面
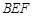 与平面
与平面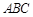 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.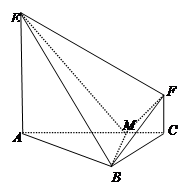
(1)见解析
(2)平面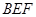 与平面
与平面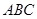 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为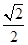
(2)平面
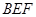 与平面
与平面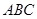 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为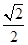
本试题主要是考查了立体几何中线线垂直的证明,以及二面角的求解,综合考查了同同学们的空间想象的能力和逻辑推理能力和计算能力的运用。灵活运用定理和性质来解决问题的运用。
(1)对于线线垂直的判定,一般通过线面垂直的性质定理得到。关键是判定BM垂直于平面ACEF
(2)建立适当的坐标系,运用坐标表示平面的法向量,利用法向量与法向量的夹角来求解二面角的平面角的问题。
解:(法一)(1)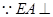 平面
平面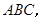
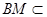 平面
平面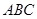 ,
,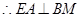 .……………1分
.……………1分
又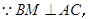
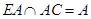 ,
,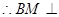 平面
平面
而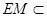 平面
平面
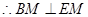 . ………………………………………3分
. ………………………………………3分
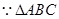 是直角三角形,
是直角三角形,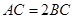 ,
,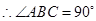 .
.
又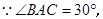
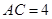 ,
,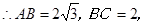
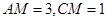 .
.
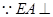 平面
平面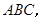
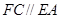 ,
,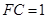 ,
, 平面
平面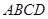 .
.
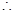
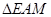 与
与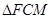 都是等腰直角三角形.
都是等腰直角三角形.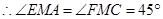 .
.
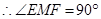 ,即
,即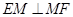 (也可由勾股定理证得).………………………………5分
(也可由勾股定理证得).………………………………5分
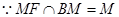 ,
,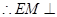 平面
平面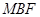 .而
.而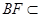 平面
平面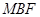 ,
,
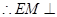
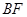 . ………………………………………………………………………………6分
. ………………………………………………………………………………6分
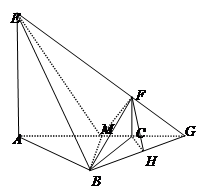
(2)延长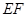 交
交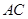 于
于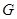 ,连
,连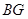 ,过
,过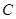 作
作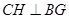 ,连结
,连结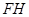 .
.
由(1)知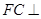 平面
平面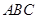 ,
,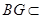 平面
平面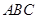 ,
,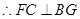 .
.
而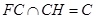 ,
, 平面
平面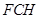 .
.
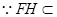 平面
平面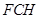 ,
,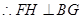 ,
,
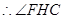 为平面
为平面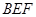 与平面
与平面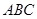 所成的二面角的平面角. ……………………8分
所成的二面角的平面角. ……………………8分
在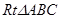 中,
中,
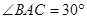 ,
,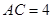 ,
,
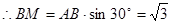 .
.
由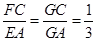 ,得
,得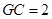 .
.
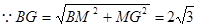 .
.
又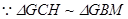 ,
,
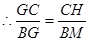 ,则
,则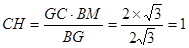 . ………………………………11分
. ………………………………11分
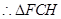 是等腰直角三角形,
是等腰直角三角形,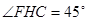 .
.
 平面
平面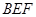 与平面
与平面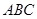 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为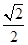 ………………………12分
………………………12分
(法二)(1)同法一,得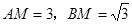 . ………………………3分
. ………………………3分
如图,以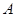 为坐标原点,垂直于
为坐标原点,垂直于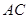 、
、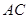 、
、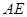 所在的直线为
所在的直线为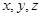 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由已知条件得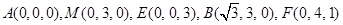 ,
,
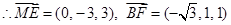 . ………4分
. ………4分
由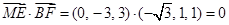 ,
,
得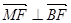 ,
, 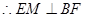 . ……………6分
. ……………6分
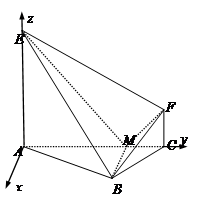
(2)由(1)知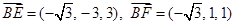 .
.
设平面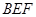 的法向量为
的法向量为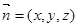 ,
,
由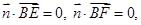 得
得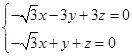 ,
,
令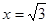 得
得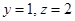 ,
,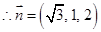 , …………………………9分
, …………………………9分
由已知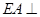 平面
平面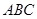 ,所以取面
,所以取面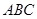 的法向量为
的法向量为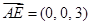 ,
,
设平面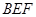 与平面
与平面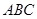 所成的锐二面角为
所成的锐二面角为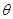 ,
,
则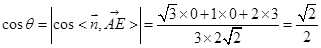 , …………………………11分
, …………………………11分
 平面
平面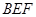 与平面
与平面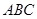 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为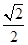 . ……………………12分
. ……………………12分
(1)对于线线垂直的判定,一般通过线面垂直的性质定理得到。关键是判定BM垂直于平面ACEF
(2)建立适当的坐标系,运用坐标表示平面的法向量,利用法向量与法向量的夹角来求解二面角的平面角的问题。
解:(法一)(1)
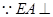 平面
平面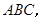
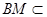 平面
平面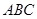 ,
,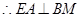 .……………1分
.……………1分又
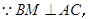
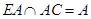 ,
,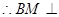 平面
平面
而
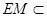 平面
平面
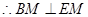 . ………………………………………3分
. ………………………………………3分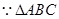 是直角三角形,
是直角三角形,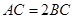 ,
,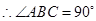 .
.又
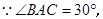
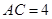 ,
,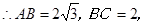
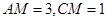 .
.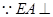 平面
平面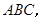
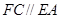 ,
,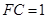 ,
, 平面
平面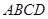 .
.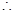
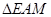 与
与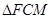 都是等腰直角三角形.
都是等腰直角三角形.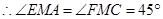 .
.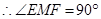 ,即
,即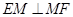 (也可由勾股定理证得).………………………………5分
(也可由勾股定理证得).………………………………5分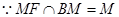 ,
,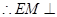 平面
平面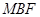 .而
.而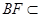 平面
平面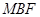 ,
,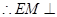
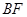 . ………………………………………………………………………………6分
. ………………………………………………………………………………6分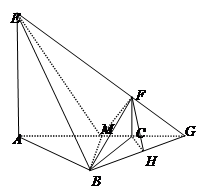
(2)延长
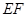 交
交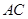 于
于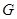 ,连
,连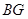 ,过
,过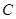 作
作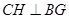 ,连结
,连结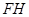 .
.由(1)知
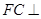 平面
平面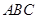 ,
,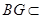 平面
平面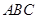 ,
,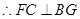 .
.而
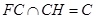 ,
, 平面
平面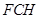 .
.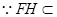 平面
平面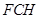 ,
,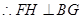 ,
,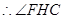 为平面
为平面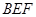 与平面
与平面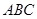 所成的二面角的平面角. ……………………8分
所成的二面角的平面角. ……………………8分在
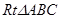 中,
中,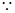
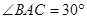 ,
,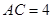 ,
,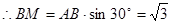 .
.由
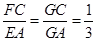 ,得
,得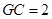 .
.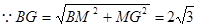 .
.又
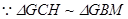 ,
,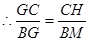 ,则
,则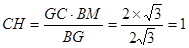 . ………………………………11分
. ………………………………11分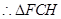 是等腰直角三角形,
是等腰直角三角形, .
. 平面
平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为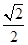 ………………………12分
………………………12分(法二)(1)同法一,得
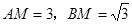 . ………………………3分
. ………………………3分如图,以
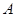 为坐标原点,垂直于
为坐标原点,垂直于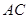 、
、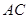 、
、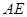 所在的直线为
所在的直线为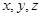 轴建立空间直角坐标系.
轴建立空间直角坐标系.由已知条件得
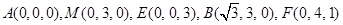 ,
,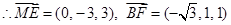 . ………4分
. ………4分由
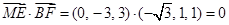 ,
,得
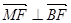 ,
, 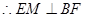 . ……………6分
. ……………6分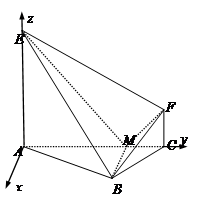
(2)由(1)知
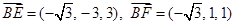 .
.设平面
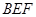 的法向量为
的法向量为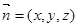 ,
,由
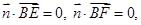 得
得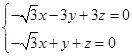 ,
,令
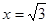 得
得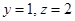 ,
,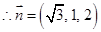 , …………………………9分
, …………………………9分由已知
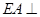 平面
平面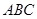 ,所以取面
,所以取面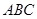 的法向量为
的法向量为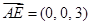 ,
,设平面
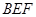 与平面
与平面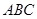 所成的锐二面角为
所成的锐二面角为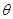 ,
,则
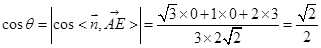 , …………………………11分
, …………………………11分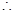 平面
平面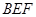 与平面
与平面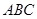 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为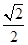 . ……………………12分
. ……………………12分
练习册系列答案
相关题目
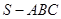 中,底面
中,底面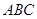 是边长为4的正三角形,平面
是边长为4的正三角形,平面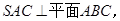
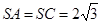 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.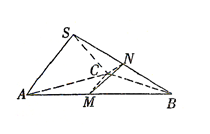
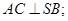
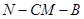 的余弦值.
的余弦值. 的底面为菱形,且
的底面为菱形,且 ,
,
 .
.
 平面
平面 ;
; 的余弦值.
的余弦值.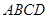 和正
和正
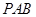 所在平面互相垂直,其中
所在平面互相垂直,其中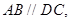
 ,且
,且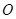 为
为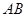 中点.
中点. 
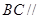 平面
平面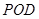 ;
;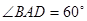 ,求二面角
,求二面角 的余弦值;
的余弦值;
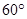 的菱形
的菱形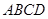 沿较短对角线
沿较短对角线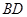 折成四面体
折成四面体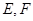 分别为
分别为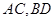 的中点,则下列命题中正确的是 。
的中点,则下列命题中正确的是 。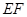 ∥
∥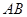 ;②
;②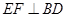 ;③
;③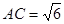 ; ⑤
; ⑤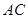 垂直于截面
垂直于截面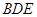 .
.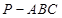 中,直线
中,直线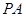 与
与 所成的角的大小为
所成的角的大小为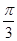
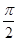
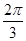
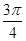
 ,则
,则


 ,
,

 ,
, ,则
,则

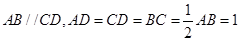 ,E为AB的中点,将
,E为AB的中点,将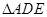 沿
沿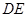 折起,使点A移至点P,若平面
折起,使点A移至点P,若平面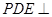 平面
平面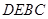 ,则D点到平面
,则D点到平面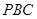 的距离是( )
的距离是( )