题目内容
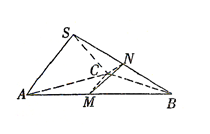
(本小题满分12分)如图,在三棱锥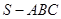 中,底面
中,底面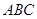 是边长为4的正三角形,平面
是边长为4的正三角形,平面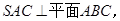
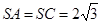 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
(1)求证: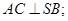
(2)求二面角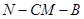 的余弦值.
的余弦值.
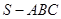 中,底面
中,底面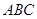 是边长为4的正三角形,平面
是边长为4的正三角形,平面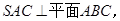
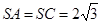 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
(1)求证:
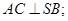
(2)求二面角
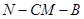 的余弦值.
的余弦值.(1)见解析;(2)余弦值为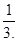
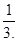
本试题主要是考查了立体几何中垂直的证明,以及二面角的求解的综合运用。
(1)(利用线面垂直的性质定理得到线线垂直,这是一般证明的方法和解题四轮。关键是证明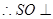 平面
平面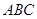 ,得到
,得到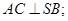
(2)合理的建立空间直角坐标系,然后表示平面的法向量和法向量的夹角,从而得到二面角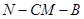 的余弦值的大小。
的余弦值的大小。
解:(1)取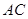 的中点O,连接
的中点O,连接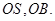
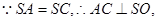
又平面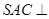 平面
平面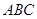 ,且平面
,且平面 平面
平面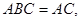
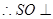 平面
平面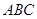 . 又
. 又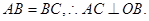 ………………………2分
………………………2分
如图所示,建立空间直角坐标系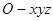 ,
,
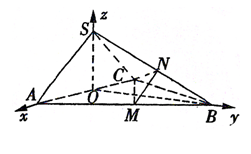
则A(2,0,0),B(0,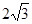 ,0),C(-2,0,0),S(0,0,
,0),C(-2,0,0),S(0,0,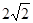 ),M(1,
),M(1,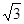 ,0),
,0),
N(0,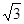 ,
,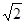 ).……4分
).……4分
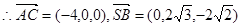 ,
,
则 ………………………6分
………………………6分
(2)由(1)得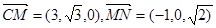 .设
.设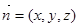 为平面
为平面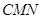 的一个法向量,
的一个法向量,
则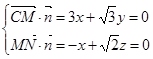 ,取
,取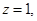 得
得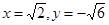 .…………………………8分
.…………………………8分
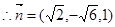 .又
.又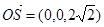 为平面
为平面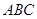 的一个法向量,
的一个法向量,
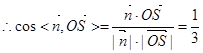 ……………………………………………………12分
……………………………………………………12分
 二面角
二面角 的余弦值为
的余弦值为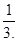
(1)(利用线面垂直的性质定理得到线线垂直,这是一般证明的方法和解题四轮。关键是证明
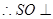 平面
平面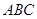 ,得到
,得到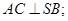
(2)合理的建立空间直角坐标系,然后表示平面的法向量和法向量的夹角,从而得到二面角
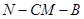 的余弦值的大小。
的余弦值的大小。解:(1)取
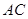 的中点O,连接
的中点O,连接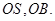
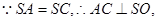
又平面
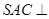 平面
平面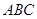 ,且平面
,且平面 平面
平面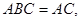
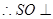 平面
平面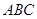 . 又
. 又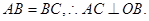 ………………………2分
………………………2分如图所示,建立空间直角坐标系
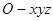 ,
,
则A(2,0,0),B(0,
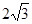 ,0),C(-2,0,0),S(0,0,
,0),C(-2,0,0),S(0,0,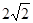 ),M(1,
),M(1,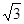 ,0),
,0),N(0,
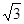 ,
,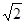 ).……4分
).……4分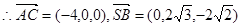 ,
,则
 ………………………6分
………………………6分(2)由(1)得
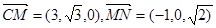 .设
.设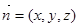 为平面
为平面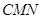 的一个法向量,
的一个法向量,则
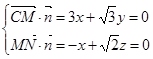 ,取
,取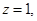 得
得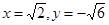 .…………………………8分
.…………………………8分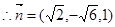 .又
.又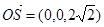 为平面
为平面 的一个法向量,
的一个法向量, ……………………………………………………12分
……………………………………………………12分 二面角
二面角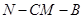 的余弦值为
的余弦值为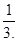

练习册系列答案
相关题目
 的底面边长为
的底面边长为 ,
, 为
为 中点.
中点.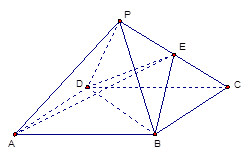
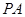 //平面
//平面 ;
; 是二面角
是二面角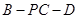 的平面角,求直线
的平面角,求直线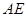 与平面
与平面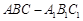 中,
中,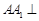 平面
平面 ,
,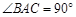 ,
,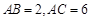 , 点
, 点 在线段
在线段 上,且
上,且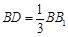 ,
,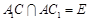 .
.
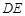 与平面
与平面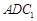 与平面
与平面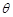 ,若
,若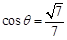 ,求
,求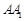 的长;
的长;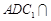 平面
平面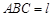 ,求直线
,求直线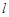 与
与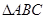 是直角三角形,
是直角三角形,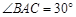 ,
,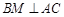 交
交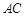 于点
于点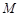 ,
,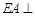 平面
平面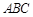 ,
,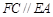 ,
,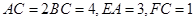 .
. ;
; 与平面
与平面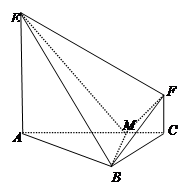
 ,
,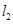 ,
,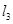 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )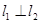 ,
,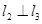
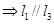
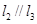
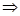
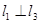
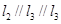
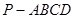 中,
中,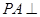 底面
底面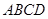 ,
,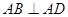 ,
,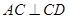 ,
,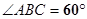 ,
,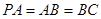 ,
,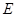 是
是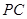 的中点.
的中点.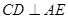 ;
;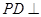 平面
平面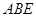 ;
;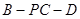 的余弦值.
的余弦值.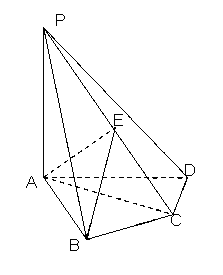
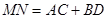
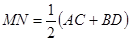
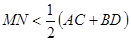
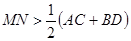
 平面α,直线c
平面α,直线c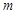 ,
,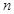 是两条不同的直线,
是两条不同的直线,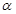 ,
,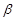 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )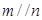 ,
,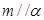 ,则
,则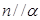 ;
;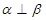 ,
,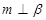 ;
;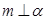 ,
,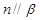 ,则
,则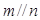 ;
;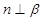 ,则
,则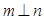 .
.