题目内容
(本小题满分12分)
如图:梯形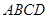 和正
和正
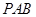 所在平面互相垂直,其中
所在平面互相垂直,其中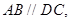
 ,且
,且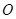 为
为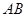 中点.
中点.

(Ⅰ) 求证: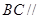 平面
平面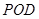 ;
;
(Ⅱ)若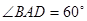 ,求二面角
,求二面角 的余弦值;
的余弦值;
如图:梯形
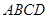 和正
和正
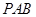 所在平面互相垂直,其中
所在平面互相垂直,其中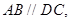
 ,且
,且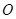 为
为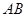 中点.
中点. 
(Ⅰ) 求证:
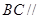 平面
平面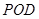 ;
;(Ⅱ)若
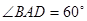 ,求二面角
,求二面角 的余弦值;
的余弦值;(1)见解析;(2)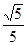 .
.
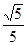 .
.要求证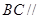 平面
平面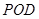 ,只需证明
,只需证明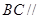 平面
平面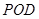 内的一直线,在说明BC不在面
内的一直线,在说明BC不在面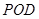 内,本题中,
内,本题中,
通过证明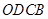 为平行四边形,得出
为平行四边形,得出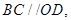 进而的证; 由
进而的证; 由 ,取AD中点E,
,取AD中点E,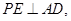 再证
再证
 ,故
,故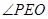 是二面角
是二面角 的平面角,转化为三角形内求解。
的平面角,转化为三角形内求解。
证明: (Ⅰ)因为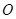 为
为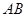 中点,
中点,
所以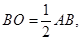 ………1分
………1分
又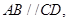
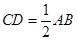 ,
,
所以有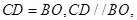 …………………2分
…………………2分
所以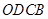 为平行四边形,所以
为平行四边形,所以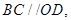 ………3分
………3分
又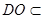 平面
平面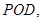
 平面
平面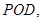
所以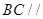 平面
平面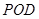 . ………5分
. ………5分
(Ⅱ)取AD的中点E,连接OE、PE,设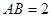 ,则
,则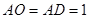
又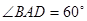 ,
,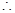
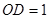
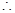
 ,
,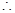
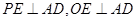
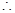
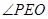 是二面角
是二面角 的平面角 9分
的平面角 9分
在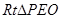 中,
中,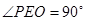 ,
,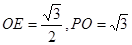 ,
,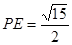
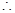
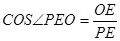
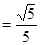 11分
11分
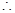 二面角
二面角 的余弦值为
的余弦值为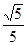 。 12分
。 12分
(其它解法酌情给分)
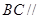 平面
平面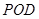 ,只需证明
,只需证明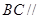 平面
平面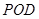 内的一直线,在说明BC不在面
内的一直线,在说明BC不在面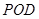 内,本题中,
内,本题中,通过证明
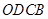 为平行四边形,得出
为平行四边形,得出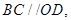 进而的证; 由
进而的证; 由 ,取AD中点E,
,取AD中点E,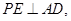 再证
再证 ,故
,故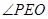 是二面角
是二面角 的平面角,转化为三角形内求解。
的平面角,转化为三角形内求解。证明: (Ⅰ)因为
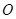 为
为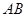 中点,
中点,所以
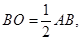 ………1分
………1分又
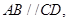
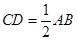 ,
,所以有
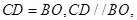 …………………2分
…………………2分所以
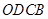 为平行四边形,所以
为平行四边形,所以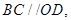 ………3分
………3分又
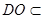 平面
平面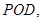
 平面
平面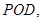
所以
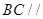 平面
平面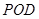 . ………5分
. ………5分(Ⅱ)取AD的中点E,连接OE、PE,设
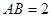 ,则
,则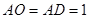
又
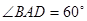 ,
,
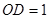
 ,
,
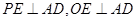
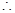
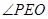 是二面角
是二面角 的平面角 9分
的平面角 9分在
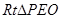 中,
中,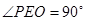 ,
,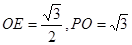 ,
,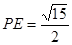
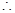
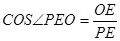
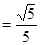 11分
11分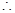 二面角
二面角 的余弦值为
的余弦值为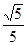 。 12分
。 12分(其它解法酌情给分)

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
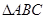 是直角三角形,
是直角三角形,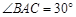 ,
,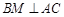 交
交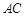 于点
于点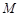 ,
,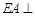 平面
平面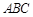 ,
,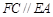 ,
,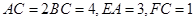 .
.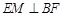 ;
;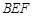 与平面
与平面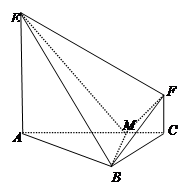
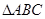 中,若
中,若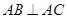 ,
,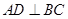 于
于 ,则
,则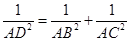 .在四面体
.在四面体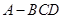 中,若
中,若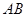 ,
,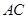 ,
,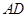 两两垂直,
两两垂直,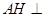 底面
底面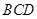 ,垂足为
,垂足为 ,则类似的结论是什么?并说明理由.
,则类似的结论是什么?并说明理由.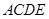 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
. 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;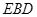 与平面
与平面 的余弦值。
的余弦值。
 中,
中, ,直线
,直线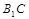 与平面
与平面 成30°角.
成30°角. 平面
平面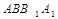 ;
; 与平面
与平面 所成角的正弦值;
所成角的正弦值; 的平面角的余弦值.
的平面角的余弦值.
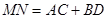
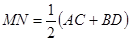
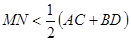
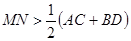
 、
、 、
、 和直线
和直线 、
、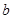 、m、n,下列命题中真命题是
、m、n,下列命题中真命题是 ,则
,则
 ,则
,则
 ,则
,则
 则
则
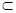 平面α,直线c
平面α,直线c 为两条不同的直线,
为两条不同的直线, 、
、 为两个不同的平面,则下列命题正确的是
为两个不同的平面,则下列命题正确的是 ;
;

