题目内容
【题目】某几何体的三视图如图所示（单位：cm），则该几何体的表面积是cm2 ， 体积是cm3 ．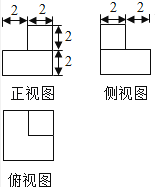 
【答案】80；40
【解析】解：根据几何体的三视图，得；
该几何体是下部为长方体，其长和宽都为4，高为2，
表面积为2×4×4+2×42=64cm2 ， 体积为2×42=32cm3；
上部为正方体，其棱长为2，
表面积是6×22=24 cm2 ， 体积为23=8cm3；
所以几何体的表面积为64+24﹣2×22=80cm2 ，
体积为32+8=40cm3 ．
故答案为：80；40．
根据几何体的三视图，得出该几何体下部为长方体，上部为正方体的组合体，结合图中数据求出它的表面积和体积即可．本题考查了由三视图求几何体的表面积与体积的应用问题，也考查了空间想象和计算能力，是基础题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
【题目】某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示，考虑以下结论：
甲 | 乙 | ||||||||
8 | 0 | ||||||||
4 3 3 | 6 6 8 | 3 8 9 1 | 1 2 3 4 5 | 2 5 1 4 0 | 5 4 6 9 | 1 | 6 | 7 | 9 |
①甲运动员得分的中位数大于乙运动员
得分的中位数；
②甲运动员得分的中位数小于乙运动员
得分的中位数；
③甲运动员得分的标准差大于乙运动员
得分的标准差；
④甲运动员得分的标准差小于乙运动员
得分的标准差；
其中根据茎叶图能得到的正确结论的编号为( )
A. ①③ B. ①④
C. ②③ D. ②④
