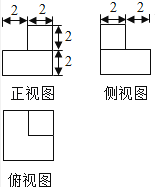
题目内容
【题目】如图，在五面体
中，已知
平面
，
，
，
，
．
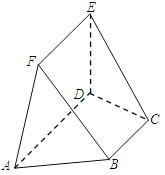
（1）求证：
；
（2）求三棱锥
的体积．
【答案】（1）详见解析，（2）
【解析】
试题分析：（1）证明线线平行，一般思路为利用线面平行的性质定理与判定定理进行转化. 因为
，
平面
，
平面，所以
平面，又
平面
，平面
平面
，所以
．（2）求三棱锥的体积，关键是找寻高.可由面面垂直性质定理探求，因为
平面
，所以有面
平面，则作
就可得
平面.证明平面过程也可从线线垂直证线面垂直.确定
是三棱锥
的高之后，可利用三棱锥的体积公式
.
试题解析：
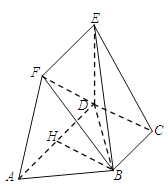
（1）因为，平面，平面，
所以平面， 3分
又平面，平面平面，
所以． 6分
（2）在平面内作于点
，
因为平面，
平面，所以
，
又
，
平面，
，
所以平面，
所以是三棱锥的高． 9分
在直角三角形
中，
，
，所以
，
因为平面，平面，所以
，
又由（1）知，，且，所以
，所以
， 12分
所以三棱锥的体积． 14分
练习册系列答案
名校课堂系列答案
相关题目
【题目】某设备的使用年数x与所支出的维修总费用y的统计数据如下表：
使用年数x（单位：年） | 2 | 3 | 4 | 5 | 6 |
维修费用y（单位：万元） | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
根据上标可得回归直线方程为 
=1.3x+ 
，若该设备维修总费用超过12万元，据此模型预测该设备最多可使用年．
