题目内容
12.已知四棱锥P-ABCD底面是平行四边形,E,F分别为AD,PC的中点,EF⊥BD,2AP=2AB=AD,以AD为直径的圆经过点B
(1)求证:平面PAB⊥平面ABCD;
(2)若AB=PB,求二面角C-BE-F的余弦值.
分析 解:(1)取PB中点G,连接AG,FG,由已知数据易证BD⊥平面PAB,进而由面面垂直的判定定理可得平面PAB⊥平面ABCD;
(2)以B为原点,BA为x轴,BD为y轴,建立如图所示的空间直角坐标系,向量法可得平面BEF的法向量$\overrightarrow{{n}_{1}}$=($\sqrt{3}$,-1,3),平面CBE的法向量$\overrightarrow{{n}_{2}}$=(0,0,1),由向量的夹角公式可得法向量夹角的余弦值,既得答案.
解答 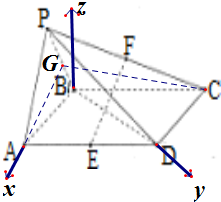 解:(1)取PB中点G,连接AG,FG,
解:(1)取PB中点G,连接AG,FG,
由三角形的中位线定理可得FG∥BC且FG=$\frac{1}{2}$BC,
∵AE∥BC且AE=$\frac{1}{2}$BC,∴FG∥AE且FG=AE,
∴AEFG是平行四边形,∴EF∥AG,
又EF⊥BD,∴AG⊥BD,
由直径所对的圆周角为90°可得∠ABD=90°,∴BD⊥AB,
又∵AG∩AB=A,∴BD⊥平面PAB,
∴平面PAB⊥平面ABCD;
(2)以B为原点,BA为x轴,BD为y轴,建立如图所示的空间直角坐标系,
令AB=2,则B(0,0,0),A(2,0,0),D(0,2$\sqrt{3}$,0),P(1,0,$\sqrt{3}$),C(-2,2$\sqrt{3}$,0),
∴$\overrightarrow{BE}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{BD}$)=(1,$\sqrt{3}$,0),$\overrightarrow{EF}$=$\overrightarrow{AG}$=$\frac{1}{2}$($\overrightarrow{AP}$+$\overrightarrow{AB}$)=$\frac{\sqrt{3}}{2}$(-$\sqrt{3}$,0,1),
设平面BEF的法向量为$\overrightarrow{{n}_{1}}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{BE}=x+\sqrt{3}y=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{EF}=-\frac{3}{2}x+\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,令x=$\sqrt{3}$可得$\overrightarrow{{n}_{1}}$=($\sqrt{3}$,-1,3),
又∵平面CBE的法向量$\overrightarrow{{n}_{2}}$=(0,0,1),
∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{3\sqrt{13}}{13}$,
∴二面角C-BE-F的余弦值为$\frac{3\sqrt{13}}{13}$.
点评 本题考查空间向量与立体几何,涉及面面垂直的判定和二面角的问题,属中档题.

 初中暑期衔接系列答案
初中暑期衔接系列答案90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
| A. | 92,2 | B. | 92,2.8 | C. | 93,2 | D. | 93,2.8 |
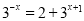 的解为_________.
的解为_________.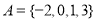 ,
,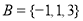 ,则
,则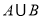 元素的个数为( )
元素的个数为( )